mjhjmtu

In mathematics, a metric space is a set together with a metric on the set. The metric is a function that defines a concept of distance between any two members of the set, which are usually called points. The metric satisfies a few simple properties. Informally:

the distance from a point to itself is zero,

the distance between two distinct points is positive,

the distance from A to B is the same as the distance from B to A, and

the distance from A to B (directly) is less than or equal to the distance from A to B via any third point C.

A metric on a space induces topological properties like open and closed sets, which lead to the study of more abstract topological spaces.

The most familiar metric space is 3-dimensional Euclidean space. In fact, a "metric" is the generalization of the Euclidean metric arising from the four long-known properties of the Euclidean distance. The Euclidean metric defines the distance between two points as the length of the straight line segment connecting them. Other metric spaces occur for example in elliptic geometry and hyperbolic geometry, where distance on a sphere measured by angle is a metric, and the hyperboloid model of hyperbolic geometry is used by special relativity as a metric space of velocities.

History

In 1906 Maurice Fréchet introduced metric spaces in his work Sur quelques points du calcul fonctionnel.^[1] However the name is due to Felix Hausdorff.

Definition

A metric space is an ordered pair $(M,d)$ where $M$ is a set and $d$ is a metric on $M$ , i.e., a function

d colon M times M to mathbbR

such that for any $x,y,zin M$ , the following holds:^[2]

1.	$displaystyle d(x,y)geq 0$	non-negativity or separation axiom
2.	$displaystyle d(x,y)=0Leftrightarrow x=y$	identity of indiscernibles
3.	$displaystyle d(x,y)=d(y,x)$	symmetry
4.	$displaystyle d(x,z)leq d(x,y)+d(y,z)$	subadditivity or triangle inequality

The first condition follows from the other three. Since for any $x, y in M$ :

$d(x,y) + d(y,x) ge d(x,x)$	by triangle inequality
$d(x,y) + d(x,y) ge d(x,x)$	by symmetry
$2d(x,y) ge 0$	by identity of indiscernibles
$d(x,y)geq 0$	we have non-negativity

The function $d$ is also called distance function or simply distance. Often, $d$ is omitted and one just writes $M$ for a metric space if it is clear from the context what metric is used.

Ignoring mathematical details, for any system of roads and terrains the distance between two locations can be defined as the length of the shortest route connecting those locations. To be a metric there shouldn't be any one-way roads. The triangle inequality expresses the fact that detours aren't shortcuts. If the distance between two points is zero, the two points are indistinguishable from one-another. Many of the examples below can be seen as concrete versions of this general idea.

Examples of metric spaces

The real numbers with the distance function $d(x,y) = vert y - x vert$ given by the absolute difference, and, more generally, Euclidean $n$ -space with the Euclidean distance, are complete metric spaces. The rational numbers with the same distance function also form a metric space, but not a complete one.

The positive real numbers with distance function $d(x,y) =vert log(y/x) vert$ is a complete metric space.

Any normed vector space is a metric space by defining d(x,y)=‖y−x‖displaystyle d(x,y)=lVert y-xrVert $d(x,y) = lVert y - x rVert$ , see also metrics on vector spaces. (If such a space is complete, we call it a Banach space.) Examples:
- The Manhattan norm gives rise to the Manhattan distance, where the distance between any two points, or vectors, is the sum of the differences between corresponding coordinates.
- The maximum norm gives rise to the Chebyshev distance or chessboard distance, the minimal number of moves a chess king would take to travel from $x$ to $y$ .

The British Rail metric (also called the “post office metric” or the “SNCF metric”) on a normed vector space is given by $d(x,y) = lVert x rVert + lVert y rVert$ for distinct points $x$ and $y$ , and $d(x,x) = 0$ . More generally $lVert . rVert$ can be replaced with a function $f$ taking an arbitrary set $S$ to non-negative reals and taking the value $displaystyle 0$ at most once: then the metric is defined on $S$ by $d(x,y) = f(x) + f(y)$ for distinct points $x$ and $y$ , and $d(x,x) = 0$ . The name alludes to the tendency of railway journeys to proceed via London (or Paris) irrespective of their final destination.

If $(M,d)$ is a metric space and $X$ is a subset of $M$ , then $(X,d)$ becomes a metric space by restricting the domain of $d$ to $Xtimes X$ .

The discrete metric, where $d(x,y) = 0$ if $x=y$ and $d(x,y) = 1$ otherwise, is a simple but important example, and can be applied to all sets. This, in particular, shows that for any set, there is always a metric space associated to it. Using this metric, any point is an open ball, and therefore every subset is open and the space has the discrete topology.

A finite metric space is a metric space having a finite number of points. Not every finite metric space can be isometrically embedded in a Euclidean space.^[3]^[4]

The hyperbolic plane is a metric space. More generally:
- If $M$ is any connected Riemannian manifold, then we can turn $M$ into a metric space by defining the distance of two points as the infimum of the lengths of the paths (continuously differentiable curves) connecting them.
- If $X$ is some set and $M$ is a metric space, then, the set of all bounded functions $f colon X rightarrow M$ (i.e. those functions whose image is a bounded subset of $M$ ) can be turned into a metric space by defining $d(f,g) = sup_x in X d(f(x),g(x))$ for any two bounded functions $f$ and $g$ (where $sup$ is supremum).^[5] This metric is called the uniform metric or supremum metric, and If $M$ is complete, then this function space is complete as well. If X is also a topological space, then the set of all bounded continuous functions from $X$ to $M$ (endowed with the uniform metric), will also be a complete metric if M is.
- If $G$ is an undirected connected graph, then the set $V$ of vertices of $G$ can be turned into a metric space by defining $d(x,y)$ to be the length of the shortest path connecting the vertices $x$ and $y$ . In geometric group theory this is applied to the Cayley graph of a group, yielding the word metric.

Graph edit distance is a measure of dissimilarity between two graphs, defined as the minimal number of graph edit operations required to transform one graph into another.

The Levenshtein distance is a measure of the dissimilarity between two strings $u$ and $v$ , defined as the minimal number of character deletions, insertions, or substitutions required to transform $u$ into $v$ . This can be thought of as a special case of the shortest path metric in a graph and is one example of an edit distance.

Given a metric space $(X,d)$ and an increasing concave function $f colon [0,infty) rightarrow [0,infty)$ such that $f(x) = 0$ if and only if $x=0$ , then $f circ d$ is also a metric on $X$ .

Given an injective function $f$ from any set $A$ to a metric space $(X,d)$ , $d(f(x), f(y))$ defines a metric on $A$ .

Using T-theory, the tight span of a metric space is also a metric space. The tight span is useful in several types of analysis.

The set of all $m$ by $n$ matrices over some field is a metric space with respect to the rank distance $d(X,Y) = mathrmrank(Y - X)$ .

The Helly metric is used in game theory.

Open and closed sets, topology and convergence

Every metric space is a topological space in a natural manner, and therefore all definitions and theorems about general topological spaces also apply to all metric spaces.

About any point $x$ in a metric space $M$ we define the open ball of radius $r > 0$ (where $r$ is a real number) about $x$ as the set

B(x;r) = y in M : d(x,y) < r.

These open balls form the base for a topology on M, making it a topological space.

Explicitly, a subset $U$ of $M$ is called open if for every $x$ in $U$ there exists an $r > 0$ such that $B(x;r)$ is contained in $U$ . The complement of an open set is called closed. A neighborhood of the point $x$ is any subset of $M$ that contains an open ball about $x$ as a subset.

A topological space which can arise in this way from a metric space is called a metrizable space; see the article on metrization theorems for further details.

A sequence ( $x_n$ ) in a metric space $M$ is said to converge to the limit $xin M$ iff for every $epsilon >0$ , there exists a natural number N such that $d(x_n,x) < epsilon$ for all $n>N$ . Equivalently, one can use the general definition of convergence available in all topological spaces.

A subset $A$ of the metric space $M$ is closed iff every sequence in $A$ that converges to a limit in $M$ has its limit in $A$ .

Types of metric spaces

Complete spaces

A metric space $M$ is said to be complete if every Cauchy sequence converges in $M$ . That is to say: if $d(x_n, x_m) to 0$ as both $n$ and $m$ independently go to infinity, then there is some $yin M$ with $d(x_n, y) to 0$ .

Every Euclidean space is complete, as is every closed subset of a complete space. The rational numbers, using the absolute value metric $d(x,y) = vert x - y vert$ , are not complete.

Every metric space has a unique (up to isometry) completion, which is a complete space that contains the given space as a dense subset. For example, the real numbers are the completion of the rationals.

If $X$ is a complete subset of the metric space $M$ , then $X$ is closed in $M$ . Indeed, a space is complete iff it is closed in any containing metric space.

Every complete metric space is a Baire space.

Bounded and totally bounded spaces

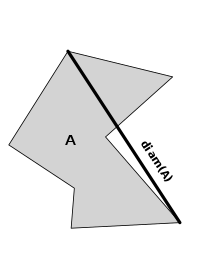
Diameter of a set.

A metric space M is called bounded if there exists some number r, such that d(x,y) ≤ r for all x and y in M. The smallest possible such r is called the diameter of M. The space M is called precompact or totally bounded if for every r > 0 there exist finitely many open balls of radius r whose union covers M. Since the set of the centres of these balls is finite, it has finite diameter, from which it follows (using the triangle inequality) that every totally bounded space is bounded. The converse does not hold, since any infinite set can be given the discrete metric (one of the examples above) under which it is bounded and yet not totally bounded.

Note that in the context of intervals in the space of real numbers and occasionally regions in a Euclidean space $displaystyle mathbb R ^n$ a bounded set is referred to as "a finite interval" or "finite region". However boundedness should not in general be confused with "finite", which refers to the number of elements, not to how far the set extends; finiteness implies boundedness, but not conversely. Also note that an unbounded subset of $displaystyle mathbb R ^n$ may have a finite volume.

Compact spaces

A metric space M is compact if every sequence in M has a subsequence that converges to a point in M. This is known as sequential compactness and, in metric spaces (but not in general topological spaces), is equivalent to the topological notions of countable compactness and compactness defined via open covers.

Examples of compact metric spaces include the closed interval [0,1] with the absolute value metric, all metric spaces with finitely many points, and the Cantor set. Every closed subset of a compact space is itself compact.

A metric space is compact iff it is complete and totally bounded. This is known as the Heine–Borel theorem. Note that compactness depends only on the topology, while boundedness depends on the metric.

Lebesgue's number lemma states that for every open cover of a compact metric space M, there exists a "Lebesgue number" δ such that every subset of M of diameter < δ is contained in some member of the cover.

Every compact metric space is second countable,^[6] and is a continuous image of the Cantor set. (The latter result is due to Pavel Alexandrov and Urysohn.)

Locally compact and proper spaces

A metric space is said to be locally compact if every point has a compact neighborhood. Euclidean spaces are locally compact, but infinite-dimensional Banach spaces are not.

A space is proper if every closed ball y : d(x,y) ≤ r is compact. Proper spaces are locally compact, but the converse is not true in general.

Connectedness

A metric space $M$ is connected if the only subsets that are both open and closed are the empty set and $M$ itself.

A metric space $M$ is path connected if for any two points $x, y in M$ there exists a continuous map $fcolon [0,1] to M$ with $f(0)=x$ and $f(1)=y$ .
Every path connected space is connected, but the converse is not true in general.

There are also local versions of these definitions: locally connected spaces and locally path connected spaces.

Simply connected spaces are those that, in a certain sense, do not have "holes".

Separable spaces

A metric space is separable space if it has a countable dense subset. Typical examples are the real numbers or any Euclidean space. For metric spaces (but not for general topological spaces) separability is equivalent to second-countability and also to the Lindelöf property.

Pointed metric spaces

If $X$ is a nonempty metric space and $x_0in X$ then $(X,x_0)$ is called a pointed metric space, and $x_0$ is called a distinguished point. Note that a pointed metric space is just a nonempty metric space with attention drawn to its distinguished point, and that any nonempty metric space can be viewed as a pointed metric space. The distinguished point is sometimes denoted $displaystyle 0$ due to its similar behavior to zero in certain contexts.

Types of maps between metric spaces

Suppose (M₁,d₁) and (M₂,d₂) are two metric spaces.

Continuous maps

The map f:M₁→M₂ is continuous
if it has one (and therefore all) of the following equivalent properties:

General topological continuity

for every open set U in M₂, the preimage f^-1(U) is open in M₁

This is the general definition of continuity in topology.

Sequential continuity

if (x_n) is a sequence in M₁ that converges to x in M₁, then the sequence (f(x_n)) converges to f(x) in M₂.

This is sequential continuity, due to Eduard Heine.

ε-δ definition

for every x in M₁ and every ε>0 there exists δ>0 such that for all y in M₁ we have

d_1(x,y)<delta Rightarrow d_2(f(x),f(y))< varepsilon.

This uses the (ε, δ)-definition of limit, and is due to Augustin Louis Cauchy.

Moreover, f is continuous if and only if it is continuous on every compact subset of M₁.

The image of every compact set under a continuous function is compact, and the image of every connected set under a continuous function is connected.

Uniformly continuous maps

The map ƒ : M₁ → M₂ is uniformly continuous if for every ε > 0 there exists δ > 0 such that

d_1(x,y)<delta Rightarrow d_2(f(x),f(y))< varepsilon quadmboxfor allquad x,yin M_1.

Every uniformly continuous map ƒ : M₁ → M₂ is continuous. The converse is true if M₁ is compact (Heine–Cantor theorem).

Uniformly continuous maps turn Cauchy sequences in M₁ into Cauchy sequences in M₂. For continuous maps this is generally wrong; for example, a continuous map
from the open interval (0,1) onto the real line turns some Cauchy sequences into unbounded sequences.

Lipschitz-continuous maps and contractions

Given a real number K > 0, the map ƒ : M₁ → M₂ is K-Lipschitz continuous if

d_2(f(x),f(y))leq K d_1(x,y)quadmboxfor allquad x,yin M_1.

Every Lipschitz-continuous map is uniformly continuous, but the converse is not true in general.

If K < 1, then ƒ is called a contraction. Suppose M₂ = M₁ and M₁ is complete. If ƒ is a contraction, then ƒ admits a unique fixed point (Banach fixed point theorem). If M₁ is compact, the condition can be weakened a bit: ƒ admits a unique fixed point if

d(f(x), f(y)) < d(x, y) quad mboxfor all quad x ne y in M_1

.

Isometries

The map f:M₁→M₂ is an isometry if

d_2(f(x),f(y))=d_1(x,y)quadmboxfor allquad x,yin M_1

Isometries are always injective; the image of a compact or complete set under an isometry is compact or complete, respectively. However, if the isometry is not surjective, then the image of a closed (or open) set need not be closed (or open).

Quasi-isometries

The map f : M₁ → M₂ is a quasi-isometry if there exist constants A ≥ 1 and B ≥ 0 such that

frac1A d_2(f(x),f(y))-Bleq d_1(x,y)leq A d_2(f(x),f(y))+B text for all x,yin M_1

and a constant C ≥ 0 such that every point in M₂ has a distance at most C from some point in the image f(M₁).

Note that a quasi-isometry is not required to be continuous. Quasi-isometries compare the "large-scale structure" of metric spaces; they find use in geometric group theory in relation to the word metric.

Notions of metric space equivalence

Given two metric spaces (M₁, d₁) and (M₂, d₂):

They are called homeomorphic (topologically isomorphic) if there exists a homeomorphism between them (i.e., a bijection continuous in both directions).

They are called uniformic (uniformly isomorphic) if there exists a uniform isomorphism between them (i.e., a bijection uniformly continuous in both directions).

They are called isometric if there exists a bijective isometry between them. In this case, the two metric spaces are essentially identical.

They are called quasi-isometric if there exists a quasi-isometry between them.

Topological properties

Metric spaces are paracompact^[7]Hausdorff spaces^[8] and hence normal (indeed they are perfectly normal). An important consequence is that every metric space admits partitions of unity and that every continuous real-valued function defined on a closed subset of a metric space can be extended to a continuous map on the whole space (Tietze extension theorem). It is also true that every real-valued Lipschitz-continuous map defined on a subset of a metric space can be extended to a Lipschitz-continuous map on the whole space.

Metric spaces are first countable since one can use balls with rational radius as a neighborhood base.

The metric topology on a metric space M is the coarsest topology on M relative to which the metric d is a continuous map from the product of M with itself to the non-negative real numbers.

Distance between points and sets; Hausdorff distance and Gromov metric

A simple way to construct a function separating a point from a closed set (as required for a completely regular space) is to consider the distance between the point and the set. If (M,d) is a metric space, S is a subset of M and x is a point of M, we define the distance from x to S as

d(x,S) = infd(x,s) : s in S

where

inf

represents the infimum.

Then d(x, S) = 0 if and only if x belongs to the closure of S. Furthermore, we have the following generalization of the triangle inequality:

d(x,S) leq d(x,y) + d(y,S),

which in particular shows that the map $xmapsto d(x,S)$ is continuous.

Given two subsets S and T of M, we define their Hausdorff distance to be

d_H(S,T) = max supd(s,T) : s in S , sup d(t,S) : t in T

where

sup

represents the supremum.

In general, the Hausdorff distance d_H(S,T) can be infinite. Two sets are close to each other in the Hausdorff distance if every element of either set is close to some element of the other set.

The Hausdorff distance d_H turns the set K(M) of all non-empty compact subsets of M into a metric space. One can show that K(M) is complete if M is complete.
(A different notion of convergence of compact subsets is given by the Kuratowski convergence.)

One can then define the Gromov–Hausdorff distance between any two metric spaces by considering the minimal Hausdorff distance of isometrically embedded versions of the two spaces. Using this distance, the class of all (isometry classes of) compact metric spaces becomes a metric space in its own right.

Product metric spaces

If $(M_1,d_1),ldots,(M_n,d_n)$ are metric spaces, and N is the Euclidean norm on Rⁿ, then $Big(M_1times ldots times M_n, N(d_1,ldots,d_n)Big)$ is a metric space, where the product metric is defined by

N(d_1,...,d_n)Big((x_1,ldots,x_n),(y_1,ldots,y_n)Big) = NBig(d_1(x_1,y_1),ldots,d_n(x_n,y_n)Big),

and the induced topology agrees with the product topology. By the equivalence of norms in finite dimensions, an equivalent metric is obtained if N is the taxicab norm, a p-norm, the max norm, or any other norm which is non-decreasing as the coordinates of a positive n-tuple increase (yielding the triangle inequality).

Similarly, a countable product of metric spaces can be obtained using the following metric

d(x,y)=sum_i=1^infty frac12^ifracd_i(x_i,y_i)1+d_i(x_i,y_i).

An uncountable product of metric spaces need not be metrizable. For example, $mathbfR^mathbfR$ is not first-countable and thus isn't metrizable.

Continuity of distance

In the case of a single space $(M,d)$ , the distance map $dcolon Mtimes M rightarrow R^+$ (from the definition) is uniformly continuous with respect to any of the above product metrics $N(d,d)$ , and in particular is continuous with respect to the product topology of $Mtimes M$ .

Quotient metric spaces

If M is a metric space with metric d, and ~ is an equivalence relation on M, then we can endow the quotient set M/~ with the following (pseudo)metric. Given two equivalence classes [x] and [y], we define

d'([x],[y]) = infd(p_1,q_1)+d(p_2,q_2)+dotsb+d(p_n,q_n)

where the infimum is taken over all finite sequences $(p_1, p_2, dots, p_n)$ and $(q_1, q_2, dots, q_n)$ with $[p_1]=[x]$ , $[q_n]=[y]$ , $[q_i]=[p_i+1], i=1,2,dots, n-1$ . In general this will only define a pseudometric, i.e. $d'([x],[y])=0$ does not necessarily imply that $[x]=[y]$ . However, for nice equivalence relations (e.g., those given by gluing together polyhedra along faces), it is a metric.

The quotient metric d is characterized by the following universal property. If $f:(M,d)longrightarrow(X,delta)$ is a metric map between metric spaces (that is, $delta(f(x),f(y))le d(x,y)$ for all x, y) satisfying f(x)=f(y) whenever $xsim y,$ then the induced function $overlinefcolon M/simlongrightarrow X$ , given by $overlinef([x])=f(x)$ , is a metric map $overlinefcolon (M/sim,d')longrightarrow (X,delta).$

A topological space is sequential if and only if it is a quotient of a metric space.^[9]

Generalizations of metric spaces

Every metric space is a uniform space in a natural manner, and every uniform space is naturally a topological space. Uniform and topological spaces can therefore be regarded as generalizations of metric spaces.

If we consider the first definition of a metric space given above and relax the second requirement, we arrive at the concepts of a pseudometric space or a dislocated metric space.^[10] If we remove the third or fourth, we arrive at a quasimetric space, or a semimetric space.

If the distance function takes values in the extended real number line R∪+∞, but otherwise satisfies all four conditions, then it is called an extended metric and the corresponding space is called an $infty$ -metric space. If the distance function takes values in some (suitable) ordered set (and the triangle inequality is adjusted accordingly), then we arrive at the notion of generalized ultrametric.^[10]

Approach spaces are a generalization of metric spaces, based on point-to-set distances, instead of point-to-point distances.

A continuity space is a generalization of metric spaces and posets, that can be used to unify the notions of metric spaces and domains.

A partial metric space is intended to be the least generalisation of the notion of a metric space, such that the distance of each point from itself is no longer necessarily zero.^[11]

Metric spaces as enriched categories

The ordered set $(mathbb R ,geq )$ can be seen as a category by requesting exactly one morphism $ato b$ if $ageq b$ and none otherwise. By using $+$ as the tensor product and $displaystyle 0$ as the identity, it becomes a monoidal category $R^*$ .
Every metric space $(M,d)$ can now be viewed as a category $M^*$ enriched over $R^*$ :

Set $operatorname Ob(M^*):=M$

For each $X,Yin M$ set $operatornameHom(X,Y):=d(X,Y)in operatornameOb(R^*)$

The composition morphism $operatornameHom(Y,Z)otimes operatornameHom(X,Y)to operatornameHom(X,Z)$ will be the unique morphism in $R^*$ given from the triangle inequality $d(y,z)+d(x,y)geq d(x,z)$

The identity morphism $0to operatornameHom(X,X)$ will be the unique morphism given from the fact that $0geq d(X,X)$ .

Since $R^*$ is a poset, all diagrams that are required for an enriched category commute automatically.

See the paper by F.W. Lawvere listed below.

Notes

^ Rendic. Circ. Mat. Palermo 22 (1906) 1–74

^ B. Choudhary (1992). The Elements of Complex Analysis. New Age International. p. 20. ISBN 978-81-224-0399-2..mw-parser-output cite.citationfont-style:inherit.mw-parser-output .citation qquotes:"""""""'""'".mw-parser-output .citation .cs1-lock-free abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .citation .cs1-lock-subscription abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registrationcolor:#555.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration spanborder-bottom:1px dotted;cursor:help.mw-parser-output .cs1-ws-icon abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center.mw-parser-output code.cs1-codecolor:inherit;background:inherit;border:inherit;padding:inherit.mw-parser-output .cs1-hidden-errordisplay:none;font-size:100%.mw-parser-output .cs1-visible-errorfont-size:100%.mw-parser-output .cs1-maintdisplay:none;color:#33aa33;margin-left:0.3em.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-formatfont-size:95%.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-leftpadding-left:0.2em.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-rightpadding-right:0.2em

^ Nathan Linial. Finite Metric Spaces—Combinatorics, Geometry and Algorithms, Proceedings of the ICM, Beijing 2002, vol. 3, pp573–586 Archived 2018-05-02 at the Wayback Machine

^ Open problems on embeddings of finite metric spaces, edited by Jirīı Matoušek, 2007 Archived 2010-12-26 at the Wayback Machine

^ Searcóid, p. 107.

^ "PlanetMath: a compact metric space is second countable". planetmath.org. Archived from the original on 5 February 2009. Retrieved 2 May 2018.

^ Rudin, Mary Ellen. A new proof that metric spaces are paracompact Archived 2016-04-12 at the Wayback Machine. Proceedings of the American Mathematical Society, Vol. 20, No. 2. (Feb., 1969), p. 603.

^ "metric spaces are Hausdorff". PlanetMath.

^ Goreham, Anthony. Sequential convergence in Topological Spaces Archived 2011-06-04 at the Wayback Machine. Honours' Dissertation, Queen's College, Oxford (April, 2001), p. 14

^ ^a^b Pascal Hitzler and Anthony Seda, Mathematical Aspects of Logic Programming Semantics. Chapman and Hall/CRC, 2010.

^ "Partial metrics : welcome". www.dcs.warwick.ac.uk. Archived from the original on 27 July 2017. Retrieved 2 May 2018.

References

Victor Bryant, Metric Spaces: Iteration and Application, Cambridge University Press, 1985,
ISBN 0-521-31897-1.

Dmitri Burago, Yu D Burago, Sergei Ivanov, A Course in Metric Geometry, American Mathematical Society, 2001,
ISBN 0-8218-2129-6.

Athanase Papadopoulos, Metric Spaces, Convexity and Nonpositive Curvature, European Mathematical Society, First edition 2004,
ISBN 978-3-03719-010-4. Second edition 2014,
ISBN 978-3-03719-132-3.

Mícheál Ó Searcóid, Metric Spaces, Springer Undergraduate Mathematics Series, 2006,
ISBN 1-84628-369-8.

Lawvere, F. William, "Metric spaces, generalized logic, and closed categories", [Rend. Sem. Mat. Fis. Milano 43 (1973), 135—166 (1974); (Italian summary)

This is reprinted (with author commentary) at Reprints in Theory and Applications of Categories
Also (with an author commentary) in Enriched categories in the logic of geometry and analysis. Repr. Theory Appl. Categ. No. 1 (2002), 1–37.

Weisstein, Eric W. "Product Metric". MathWorld.

External links

Hazewinkel, Michiel, ed. (2001) [1994], "Metric space", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4

Far and near — several examples of distance functions at cut-the-knot.

[1] Rendic. Circ. Mat. Palermo 22 (1906) 1–74

[2] B. Choudhary (1992). The Elements of Complex Analysis. New Age International. p. 20. ISBN 978-81-224-0399-2..mw-parser-output cite.citationfont-style:inherit.mw-parser-output .citation qquotes:"""""""'""'".mw-parser-output .citation .cs1-lock-free abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .citation .cs1-lock-subscription abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registrationcolor:#555.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration spanborder-bottom:1px dotted;cursor:help.mw-parser-output .cs1-ws-icon abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center.mw-parser-output code.cs1-codecolor:inherit;background:inherit;border:inherit;padding:inherit.mw-parser-output .cs1-hidden-errordisplay:none;font-size:100%.mw-parser-output .cs1-visible-errorfont-size:100%.mw-parser-output .cs1-maintdisplay:none;color:#33aa33;margin-left:0.3em.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-formatfont-size:95%.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-leftpadding-left:0.2em.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-rightpadding-right:0.2em

[3] Nathan Linial. Finite Metric Spaces—Combinatorics, Geometry and Algorithms, Proceedings of the ICM, Beijing 2002, vol. 3, pp573–586 Archived 2018-05-02 at the Wayback Machine

[4] Open problems on embeddings of finite metric spaces, edited by Jirīı Matoušek, 2007 Archived 2010-12-26 at the Wayback Machine

[5] Searcóid, p. 107.

[6] "PlanetMath: a compact metric space is second countable". planetmath.org. Archived from the original on 5 February 2009. Retrieved 2 May 2018.

[7] Rudin, Mary Ellen. A new proof that metric spaces are paracompact Archived 2016-04-12 at the Wayback Machine. Proceedings of the American Mathematical Society, Vol. 20, No. 2. (Feb., 1969), p. 603.

[8] "metric spaces are Hausdorff". PlanetMath.

[9] Goreham, Anthony. Sequential convergence in Topological Spaces Archived 2011-06-04 at the Wayback Machine. Honours' Dissertation, Queen's College, Oxford (April, 2001), p. 14

[auto-10] Pascal Hitzler and Anthony Seda, Mathematical Aspects of Logic Programming Semantics. Chapman and Hall/CRC, 2010.

[11] "Partial metrics : welcome". www.dcs.warwick.ac.uk. Archived from the original on 27 July 2017. Retrieved 2 May 2018.

v t e Topology
Fields	General (point-set) Algebraic Combinatorial Continuum Differential Geometric low-dimensional Homology cohomology Set-theoretic
Key concepts	Open set / Closed set Continuity Space compact Hausdorff metric uniform Homotopy homotopy group fundamental group Simplicial complex CW complex Manifold
Category Portal Wikibook Wikiversity Topics general algebraic geometric Publications

搜尋此網誌