Cube
| Regular hexahedron | |
|---|---|
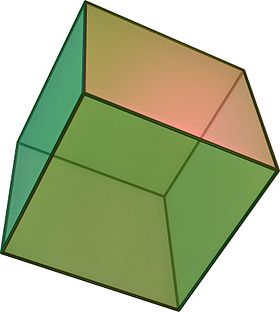 (Click here for rotating model) | |
| Type | Platonic solid |
| Elements | F = 6, E = 12 V = 8 (χ = 2) |
| Faces by sides | 64 |
| Conway notation | C |
| Schläfli symbols | 4,3 |
| t2,4 or 4× tr2,2 or ×× | |
| Face configuration | V3.3.3.3 |
| Wythoff symbol | 3 | 2 4 |
| Coxeter diagram | |
| Symmetry | Oh, B3, [4,3], (*432) |
| Rotation group | O, [4,3]+, (432) |
| References | U06, C18, W3 |
| Properties | regular, convexzonohedron |
| Dihedral angle | 90° |
 4.4.4 (Vertex figure) |  Octahedron (dual polyhedron) |
 Net | |

Net of cube
In geometry, a cube[1] is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex.
The cube is the only regular hexahedron and is one of the five Platonic solids. It has 6 faces, 12 edges, and 8 vertices.
The cube is also a square parallelepiped, an equilateral cuboid and a right rhombohedron. It is a regular square prism in three orientations, and a trigonal trapezohedron in four orientations.
The cube is dual to the octahedron. It has cubical or octahedral symmetry.
The cube is the only convex polyhedron whose faces are all squares.
Contents
1 Orthogonal projections
2 Spherical tiling
3 Cartesian coordinates
4 Equation in R3
5 Formulas
5.1 Point in space
6 Doubling the cube
7 Uniform colorings and symmetry
8 Geometric relations
9 Other dimensions
10 Related polyhedra
10.1 In uniform honeycombs and polychora
11 Cubical graph
12 See also
13 References
14 External links
Orthogonal projections
The cube has four special orthogonal projections, centered, on a vertex, edges, face and normal to its vertex figure. The first and third correspond to the A2 and B2Coxeter planes.
| Centered by | Face | Vertex |
|---|---|---|
| Coxeter planes | B2  | A2  |
| Projective symmetry | [4] | [6] |
| Tilted views |  |  |
Spherical tiling
The cube can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.
 |  |
Orthographic projection | Stereographic projection |
|---|
Cartesian coordinates
For a cube centered at the origin, with edges parallel to the axes and with an edge length of 2, the Cartesian coordinates of the vertices are
- (±1, ±1, ±1)
while the interior consists of all points (x0, x1, x2) with −1 < xi < 1 for all i.
Equation in R3
In analytic geometry, a cube's surface with center (x0, y0, z0) and edge length of 2a is the locus of all points (x, y, z) such that
- max,=a.displaystyle max=a.
Formulas
For a cube of edge length adisplaystyle a
surface area | 6a2displaystyle 6a^2,  | volume | a3displaystyle a^3,  |
face diagonal | 2adisplaystyle sqrt 2a  | space diagonal | 3atextstyle sqrt 3a  |
| radius of circumscribed sphere | 32adisplaystyle frac sqrt 32a  | radius of sphere tangent to edges | a2displaystyle frac asqrt 2  |
| radius of inscribed sphere | a2displaystyle frac a2  | angles between faces (in radians) | π2displaystyle frac pi 2  |
As the volume of a cube is the third power of its sides a×a×adisplaystyle atimes atimes a
A cube has the largest volume among cuboids (rectangular boxes) with a given surface area. Also, a cube has the largest volume among cuboids with the same total linear size (length+width+height).
Point in space
For a cube whose circumscribing sphere has radius R, and for a given point in its 3-dimensional space with distances di from the cube's eight vertices, we have:[2]
- ∑i=18di48+16R49=(∑i=18di28+2R23)2.displaystyle frac sum _i=1^8d_i^48+frac 16R^49=left(frac sum _i=1^8d_i^28+frac 2R^23right)^2.
Doubling the cube
Doubling the cube, or the Delian problem, was the problem posed by ancient Greek mathematicians of using only a compass and straightedge to start with the length of the edge of a given cube and to construct the length of the edge of a cube with twice the volume of the original cube. They were unable to solve this problem, and in 1837 Pierre Wantzel proved it to be impossible because the cube root of 2 is not a constructible number.
Uniform colorings and symmetry

Octahedral symmetry tree
The cube has three uniform colorings, named by the colors of the square faces around each vertex: 111, 112, 123.
The cube has three classes of symmetry, which can be represented by vertex-transitive coloring the faces. The highest octahedral symmetry Oh has all the faces the same color. The dihedral symmetry D4h comes from the cube being a prism, with all four sides being the same color. The lowest symmetry D2h is also a prismatic symmetry, with sides alternating colors, so there are three colors, paired by opposite sides. Each symmetry form has a different Wythoff symbol.
| Name | Regular hexahedron | Square prism | Rectangular cuboid | Rhombic prism | Trigonal trapezohedron | |
|---|---|---|---|---|---|---|
Coxeter diagram | ||||||
Schläfli symbol | 4,3 | 4× rr4,2 | s22,4 | 3 tr2,2 | ×2 | |
Wythoff symbol | 3 | 4 2 | 4 2 | 2 | 2 2 2 | | |||
Symmetry | Oh [4,3] (*432) | D4h [4,2] (*422) | D2d [4,2+] (2*2) | D2h [2,2] (*222) | D3d [6,2+] (2*3) | |
| Symmetry order | 24 | 16 | 8 | 8 | 12 | |
| Image (uniform coloring) |  (111) |  (112) |  (112) |  (123) |  (112) | 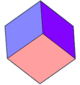 (111), (112) |
Geometric relations

The 11 nets of the cube.

These familiar six-sided dice are cube-shaped.
A cube has eleven nets (one shown above): that is, there are eleven ways to flatten a hollow cube by cutting seven edges.[3] To color the cube so that no two adjacent faces have the same color, one would need at least three colors.
The cube is the cell of the only regular tiling of three-dimensional Euclidean space. It is also unique among the Platonic solids in having faces with an even number of sides and, consequently, it is the only member of that group that is a zonohedron (every face has point symmetry).
The cube can be cut into six identical square pyramids. If these square pyramids are then attached to the faces of a second cube, a rhombic dodecahedron is obtained (with pairs of coplanar triangles combined into rhombic faces).
Other dimensions
The analogue of a cube in four-dimensional Euclidean space has a special name—a tesseract or hypercube. More properly, a hypercube (or n-dimensional cube or simply n-cube) is the analogue of the cube in n-dimensional Euclidean space and a tesseract is the order-4 hypercube. A hypercube is also called a measure polytope.
There are analogues of the cube in lower dimensions too: a point in dimension 0, a line segment in one dimension and a square in two dimensions.
Related polyhedra

The dual of a cube is an octahedron, seen here with vertices at the center of the cube's square faces.

The hemicube is the 2-to-1 quotient of the cube.
The quotient of the cube by the antipodal map yields a projective polyhedron, the hemicube.
If the original cube has edge length 1, its dual polyhedron (an octahedron) has edge length 2/2displaystyle scriptstyle sqrt 2/2
The cube is a special case in various classes of general polyhedra:
| Name | Equal edge-lengths? | Equal angles? | Right angles? |
|---|---|---|---|
| Cube | Yes | Yes | Yes |
| Rhombohedron | Yes | Yes | No |
| Cuboid | No | Yes | Yes |
| Parallelepiped | No | Yes | No |
quadrilaterally faced hexahedron | No | No | No |
The vertices of a cube can be grouped into two groups of four, each forming a regular tetrahedron; more generally this is referred to as a demicube. These two together form a regular compound, the stella octangula. The intersection of the two forms a regular octahedron. The symmetries of a regular tetrahedron correspond to those of a cube which map each tetrahedron to itself; the other symmetries of the cube map the two to each other.
One such regular tetrahedron has a volume of 1/3 of that of the cube. The remaining space consists of four equal irregular tetrahedra with a volume of 1/6 of that of the cube, each.
The rectified cube is the cuboctahedron. If smaller corners are cut off we get a polyhedron with six octagonal faces and eight triangular ones. In particular we can get regular octagons (truncated cube). The rhombicuboctahedron is obtained by cutting off both corners and edges to the correct amount.
A cube can be inscribed in a dodecahedron so that each vertex of the cube is a vertex of the dodecahedron and each edge is a diagonal of one of the dodecahedron's faces; taking all such cubes gives rise to the regular compound of five cubes.
If two opposite corners of a cube are truncated at the depth of the three vertices directly connected to them, an irregular octahedron is obtained. Eight of these irregular octahedra can be attached to the triangular faces of a regular octahedron to obtain the cuboctahedron.
The cube is topologically related to a series of spherical polyhedra and tilings with order-3 vertex figures.
| *n32 symmetry mutation of regular tilings: n,3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Spherical | Euclidean | Compact hyperb. | Paraco. | Noncompact hyperbolic | |||||||
 |  |  |  |  |  |  |  |  |  |  |  |
2,3 | 3,3 | 4,3 | 5,3 | 6,3 | 7,3 | 8,3 | ∞,3 | 12i,3 | 9i,3 | 6i,3 | 3i,3 |
The cuboctahedron is one of a family of uniform polyhedra related to the cube and regular octahedron.
Uniform octahedral polyhedra | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
Symmetry: [4,3], (*432) | [4,3]+ (432) | [1+,4,3] = [3,3] (*332) | [3+,4] (3*2) | |||||||
4,3 | t4,3 | r4,3 r31,1 | t3,4 t31,1 | 3,4 31,1 | rr4,3 s23,4 | tr4,3 | sr4,3 | h4,3 3,3 | h24,3 t3,3 | s3,4 s31,1 |
= | = | = | ||||||||
| Duals to uniform polyhedra | ||||||||||
V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
The cube is topologically related as a part of sequence of regular tilings, extending into the hyperbolic plane: 4,p, p=3,4,5...
| *n42 symmetry mutation of regular tilings: 4,n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Spherical | Euclidean | Compact hyperbolic | Paracompact | ||||||||
 4,3 |  4,4 |  4,5 |  4,6 |  4,7 |  4,8... |  4,∞ | |||||
With dihedral symmetry, Dih4, the cube is topologically related in a series of uniform polyhedra and tilings 4.2n.2n, extending into the hyperbolic plane:
| *n42 symmetry mutation of truncated tilings: 4.2n.2n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry *n42 [n,4] | Spherical | Euclidean | Compact hyperbolic | Paracomp. | |||||||
| *242 [2,4] | *342 [3,4] | *442 [4,4] | *542 [5,4] | *642 [6,4] | *742 [7,4] | *842 [8,4]... | *∞42 [∞,4] | ||||
| Truncated figures |  | 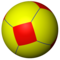 |  |  |  |  |  |  | |||
Config. | 4.4.4 | 4.6.6 | 4.8.8 | 4.10.10 | 4.12.12 | 4.14.14 | 4.16.16 | 4.∞.∞ | |||
| n-kis figures |  |  |  |  |  |  |  |  | |||
Config. | V4.4.4 | V4.6.6 | V4.8.8 | V4.10.10 | V4.12.12 | V4.14.14 | V4.16.16 | V4.∞.∞ | |||
All these figures have octahedral symmetry.
The cube is a part of a sequence of rhombic polyhedra and tilings with [n,3] Coxeter group symmetry. The cube can be seen as a rhombic hexahedron where the rhombi are squares.
| Symmetry mutations of dual quasiregular tilings: V(3.n)2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
*n32 | Spherical | Euclidean | Hyperbolic | ||||||||
| *332 | *432 | *532 | *632 | *732 | *832... | *∞32 | |||||
| Tiling |  |  |  |  |  |  |  | ||||
Conf. | V(3.3)2 | V(3.4)2 | V(3.5)2 | V(3.6)2 | V(3.7)2 | V(3.8)2 | V(3.∞)2 | ||||
The cube is a square prism:
| Family of uniform prisms | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Polyhedron | |||||||||||
Coxeter | |||||||||||
| Tiling | |||||||||||
Config. | 2.4.4 | 3.4.4 | 4.4.4 | 5.4.4 | 6.4.4 | 7.4.4 | 8.4.4 | 9.4.4 | 10.4.4 | 11.4.4 | 12.4.4 |
As a trigonal trapezohedron, the cube is related to the hexagonal dihedral symmetry family.
| Uniform hexagonal dihedral spherical polyhedra | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Symmetry: [6,2], (*622) | [6,2]+, (622) | [6,2+], (2*3) | ||||||||||||
 |  |  |  |  |  |  | ||||||||
6,2 | t6,2 | r6,2 | t2,6 | 2,6 | rr6,2 | tr6,2 | sr6,2 | s2,6 | ||||||
| Duals to uniforms | ||||||||||||||
 |  |  |  |  |  |  |  |  | ||||||
V62 | V122 | V62 | V4.4.6 | V26 | V4.4.6 | V4.4.12 | V3.3.3.6 | V3.3.3.3 | ||||||
 Compound of three cubes | 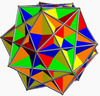 Compound of five cubes |
In uniform honeycombs and polychora
It is an element of 9 of 28 convex uniform honeycombs:
Cubic honeycomb | Truncated square prismatic honeycomb | Snub square prismatic honeycomb | Elongated triangular prismatic honeycomb | Gyroelongated triangular prismatic honeycomb |
 | 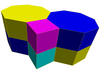 |  |  |  |
Cantellated cubic honeycomb | Cantitruncated cubic honeycomb | Runcitruncated cubic honeycomb | Runcinated alternated cubic honeycomb | |
 |  |  |  |
It is also an element of five four-dimensional uniform polychora:
Tesseract | Cantellated 16-cell | Runcinated tesseract | Cantitruncated 16-cell | Runcitruncated 16-cell |
 |  |  |  |  |
Cubical graph
| Cubical graph | |
|---|---|
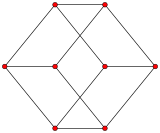 | |
| Named after | Q3 |
| Vertices | 8 |
| Edges | 12 |
| Radius | 3 |
| Diameter | 3 |
| Girth | 4 |
| Automorphisms | 48 |
| Chromatic number | 2 |
| Properties | Hamiltonian, regular, symmetric, distance-regular, distance-transitive, 3-vertex-connected, planar graph |
| Table of graphs and parameters | |
The skeleton of the cube (the vertices and edges) form a graph, with 8 vertices, and 12 edges. It is a special case of the hypercube graph.[4] It is one of 5 Platonic graphs, each a skeleton of its Platonic solid.
An extension is the three dimensional k-ary Hamming graph, which for k = 2 is the cube graph. Graphs of this sort occur in the theory of parallel processing in computers.
See also
- Tesseract
- Trapezohedron
Miscellaneous cubes
- Cube (film)
- Diamond cubic
- Lövheim cube of emotion
- Cube of Heymans
- Necker Cube
- OLAP cube
- Prince Rupert's cube
- Rubik's Cube
- The Cube (game show)
- Unit cube
- Yoshimoto Cube
- Kaaba
References
^ English cube from Old French < Latin cubus < Greek κύβος (kubos) meaning "a cube, a die, vertebra". In turn from PIE *keu(b)-, "to bend, turn".
^ Park, Poo-Sung. "Regular polytope distances", Forum Geometricorum 16, 2016, 227-232. http://forumgeom.fau.edu/FG2016volume16/FG201627.pdf
^ Weisstein, Eric W. "Cube". MathWorld..mw-parser-output cite.citationfont-style:inherit.mw-parser-output .citation qquotes:"""""""'""'".mw-parser-output .citation .cs1-lock-free abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .citation .cs1-lock-subscription abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registrationcolor:#555.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration spanborder-bottom:1px dotted;cursor:help.mw-parser-output .cs1-ws-icon abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center.mw-parser-output code.cs1-codecolor:inherit;background:inherit;border:inherit;padding:inherit.mw-parser-output .cs1-hidden-errordisplay:none;font-size:100%.mw-parser-output .cs1-visible-errorfont-size:100%.mw-parser-output .cs1-maintdisplay:none;color:#33aa33;margin-left:0.3em.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-formatfont-size:95%.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-leftpadding-left:0.2em.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-rightpadding-right:0.2em
^ Weisstein, Eric W. "Cubical graph". MathWorld.
External links
- Weisstein, Eric W. "Cube". MathWorld.
Cube: Interactive Polyhedron Model*
Volume of a cube, with interactive animation
Cube (Robert Webb's site)
Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||


