mjhjmtu

A measure of a substance's ability to resist or conduct the flow of electric current

Electrical resistivity (also known as specific electrical resistance, or volume resistivity) is a fundamental property of a material that quantifies how strongly that material opposes the flow of electric current. A low resistivity indicates a material that readily allows the flow of electric current. Resistivity is commonly represented by the Greek letter ρ (rho). The SI unit of electrical resistivity is the ohm-metre (Ω⋅m).^[1]^[2]^[3] As an example, if a 1 m × 1 m × 1 m solid cube of material has sheet contacts on two opposite faces, and the resistance between these contacts is 1 Ω, then the resistivity of the material is 1 Ω⋅m.

Electrical conductivity or specific conductance is the reciprocal of electrical resistivity, and measures a material's ability to conduct an electric current. It is commonly represented by the Greek letter σ (sigma), but κ (kappa) (especially in electrical engineering) or γ (gamma) are also occasionally used. Its SI unit is siemens per metre (S/m).

Definition

Ideal case

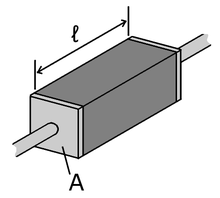
A piece of resistive material with electrical contacts on both ends.

In an ideal case, cross-section and physical composition of the examined material are uniform across the sample, and the electric field and current density are both parallel and constant everywhere. Many resistors and conductors do in fact have a uniform cross section with a uniform flow of electric current, and are made of a single material, so that this is a good model. (See the adjacent diagram.) When this is the case, the electrical resistivity ρ (Greek: rho) can be calculated by:

rho =Rfrac Aell ,,!

where

R

is the electrical resistance of a uniform specimen of the material

$ell$ is the length of the specimen

A

is the cross-sectional area of the specimen

Both resistance and resistivity describe how difficult it is to make electrical current flow through a material, but unlike resistance, resistivity is an intrinsic property. This means that all pure copper wires (which have not been subjected to distortion of their crystalline structure etc.), irrespective of their shape and size, have the same resistivity, but a long, thin copper wire has a much larger resistance than a thick, short copper wire. Every material has its own characteristic resistivity. For example, rubber has a far larger resistivity than copper.

In a hydraulic analogy, passing current through a high-resistivity material is like pushing water through a pipe full of sand—while passing current through a low-resistivity material is like pushing water through an empty pipe. If the pipes are the same size and shape, the pipe full of sand has higher resistance to flow. Resistance, however, is not solely determined by the presence or absence of sand. It also depends on the length and width of the pipe: short or wide pipes have lower resistance than narrow or long pipes.

The above equation can be transposed to get Pouillet's law (named after Claude Pouillet):

R=rho frac ell A.,!

The resistance of a given material is proportional to the length, but inversely proportional to the cross-sectional area. Thus resistivity can be expressed using the SI unit "ohm metre" (Ω⋅m) (i.e ohms divided by metres (for the length) and then multiplied by square metres (for the cross-sectional area)}.

For example, if A = 7000100000000000000♠1 m² $ell$ = 7000100000000000000♠1 m (forming a cube with perfectly conductive contacts on opposite faces), then the resistance of this element in ohms is numerically equal to the resistivity of the material it is made of in Ω⋅m.

Conductivity, σ, is the inverse of resistivity:

displaystyle sigma =frac 1rho .,!

Conductivity has SI units of "siemens per metre" (S/m).

General scalar case

For less ideal cases, such as more complicated geometry, or when the current and electric field vary in different parts of the material, it is necessary to use a more general expression in which the resistivity at a particular point is defined as the ratio of the electric field to the density of the current it creates at that point:

rho =frac EJ,,!

where

rho

is the resistivity of the conductor material,

E

is the magnitude of the electric field,

J

is the magnitude of the current density,

in which $E$ and $J$ are inside the conductor.

Conductivity is the inverse (reciprocal) of resistivity. Here, it is given by:

sigma =frac 1rho =frac JE.,!

For example, rubber is a material with large ρ and small σ—because even a very large electric field in rubber makes almost no current flow through it. On the other hand, copper is a material with small ρ and large σ—because even a small electric field pulls a lot of current through it.

As shown below, this expression simplifies to a single number when the electric field and current density are constant in the material.

Derivation from general definition of resistivity

There are three equations to be combined here. The first is the resistivity for parallel current and electric field:

rho =frac EJ,,!

If the electric field is constant, the electric field is given by the total voltage across the conductor, V, divided by length of the conductor, l:

displaystyle E=V/l

If the current density is constant, it is equal to the total current divided by the cross sectional area:

displaystyle J=I/A

Plugging in the values of E and J into the first expression, we obtain:

displaystyle rho =frac VAIl

Finally, we apply Ohm's law, V/I=R.

displaystyle rho =Rfrac Al

Tensor resistivity

When the resistivity of a material has a directional component, the most general definition of resistivity must be used. It starts from the tensor-vector form of Ohm's law which relates the electric field inside a material to the electric current flow. This equation is completely general, meaning it is valid in all cases, including those mentioned above. However, this definition is the most complicated, so it is only directly used in anisotropic cases, where the more simple definitions cannot be applied. If the material is not anisotropic, it is safe to ignore the tensor-vector definition, and use a simpler expression instead.

Here, anisotropic means that the material has different properties in different directions. For example, a crystal of graphite consists microscopically of a stack of sheets, and current flows very easily through each sheet, but much less easily from one sheet to the adjacent one.^[4] In such cases, the current does not flow in exactly the same direction as the electric field. Thus, the appropriate equations are generalized to the three-dimensional tensor form:^[5]^[6]

displaystyle mathbf J =boldsymbol sigma mathbf E ,,rightleftharpoons ,,mathbf E =boldsymbol rho mathbf J ,!

where the conductivity σ and resistivity ρ are rank-2 tensors, and electric field E and current density J are vectors. These tensors can be represented by 3×3 matrices, the vectors with 3x1 matrices, with matrix multiplication used on the right side of these equations. In matrix form, the resistivity relation is given by:

displaystyle beginbmatrixE_x\E_y\E_zendbmatrix=beginbmatrixrho _xx&rho _xy&rho _xz\rho _yx&rho _yy&rho _yz\rho _zx&rho _zy&rho _zzendbmatrixbeginbmatrixJ_x\J_y\J_zendbmatrix

where

mathbf E

is the electric field vector, with components (E_x, E_y, E_z).

boldsymbol rho

is the resistivity tensor, in general a three by three matrix.

mathbf J

is the electric current density vector, with components (J_x, J_y, J_z)

Equivalently, resistivity can be given in the more compact Einstein notation:

displaystyle mathbf E _i=boldsymbol rho _ijmathbf J _j

In either case, the resulting expression for each electric field component is:

displaystyle E_x=rho _xxJ_x+rho _xyJ_y+rho _xzJ_z

.

displaystyle E_y=rho _yxJ_x+rho _yyJ_y+rho _yzJ_z

.

displaystyle E_z=rho _zxJ_x+rho _zyJ_y+rho _zzJ_z

.

Since the choice of the coordinate system is free, the usual convention is to simplify the expression by choosing an x-axis parallel to the current direction, so J_y=J_z=0. This leaves:

displaystyle rho _xx=frac E_xJ_x

,

displaystyle rho _yx=frac E_yJ_x

, and

displaystyle rho _zx=frac E_zJ_x

Conductivity is defined similarly:^[7]

displaystyle beginbmatrixJ_x\J_y\J_zendbmatrix=beginbmatrixsigma _xx&sigma _xy&sigma _xz\sigma _yx&sigma _yy&sigma _yz\sigma _zx&sigma _zy&sigma _zzendbmatrixbeginbmatrixE_x\E_y\E_zendbmatrix

or

displaystyle mathbf J _i=boldsymbol sigma _ijmathbf E _j

Both resulting in:

displaystyle J_x=sigma _xxE_x+sigma _xyE_y+sigma _xzE_z

displaystyle J_y=sigma _yxE_x+sigma _yyE_y+sigma _yzE_z

displaystyle J_z=sigma _zxE_x+sigma _zyE_y+sigma _zzE_z

Looking at the two expressions, $boldsymbol rho$ and $boldsymbol sigma$ are the matrix inverse of each other. However, in the most general case, the individual matrix elements are not necessarily reciprocals of one another; for example, σ_xx may not be equal to 1/ρ_xx. This can be seen in the Hall effect, where $displaystyle rho _xy$ is nonzero. In the Hall effect, due to rotational invariance about the z-axis, $displaystyle rho _yy=rho _xx$ and $displaystyle rho _yx=-rho _xy$ , so the relation between resistivity and conductivity simplifies to:^[8]

displaystyle sigma _xx=frac rho _xxrho _xx^2+rho _xy^2

,

displaystyle sigma _xy=frac -rho _xyrho _xx^2+rho _xy^2

If the electric field is parallel to the applied current, $displaystyle rho _xy$ and $displaystyle rho _xz$ are zero. When they are zero, one number, $displaystyle rho _xx$ , is enough to describe the electrical resistivity. It is then written as simply $rho$ , and this reduces to the simpler expression.

Causes of conductivity

Band theory simplified

Filling of the electronic states in various types of materials at equilibrium. Here, height is energy while width is the density of available states for a certain energy in the material listed. The shade follows the Fermi–Dirac distribution (black = all states filled, white = no state filled). In metals and semimetals the Fermi level E_F lies inside at least one band. In insulators and semiconductors the Fermi level is inside a band gap; however, in semiconductors the bands are near enough to the Fermi level to be thermally populated with electrons or holes.

edit

According to elementary quantum mechanics, an electron in an atom or crystal can only have certain precise energy levels; energies between these levels are impossible. When a large number of such allowed energy levels are spaced close together (in energy-space)—i.e. have similar (minutely differing) energies— we can talk about these energy levels together as an "energy band". There can be many such energy bands in a material, depending on the atomic number number of electrons (if the atom is neutral) and their distribution (besides the size of the crystal and external factors like environmental modification of the energy bands).

The material's electrons seek to minimize the total energy in the material by going to low energy states; however, the Pauli exclusion principle means that only one can exist in each such state. So the electrons "fill up" the band structure starting from the bottom. The characteristic energy level up to which the electrons have filled is called the Fermi level. The position of the Fermi level with respect to the band structure is very important for electrical conduction: only electrons in energy levels near the Fermi level are free to move around, since the electrons can easily jump among the partially occupied states in that region. In contrast, the low energy states are rigidly filled with a fixed number of electrons at all times, and the high energy states are empty of electrons at all times.

Electric current consists of a flow of electrons. In metals there are many electron energy levels near the Fermi level, so there are many electrons available to move. This is what causes the high electronic conductivity of metals.

An important part of band theory is that there may be forbidden bands of energy: energy intervals that contain no energy levels. In insulators and semiconductors, the number of electrons is just the right amount to fill a certain integer number of low energy bands, exactly to the boundary. In this case, the Fermi level falls within a band gap. Since there are no available states near the Fermi level, and the electrons are not freely movable, the electronic conductivity is very low.

In metals

Like balls in a Newton's cradle, electrons in a metal quickly transfer energy from one terminal to another, despite their own negligible movement.

A metal consists of a lattice of atoms, each with an outer shell of electrons that freely dissociate from their parent atoms and travel through the lattice. This is also known as a positive ionic lattice.^[9] This 'sea' of dissociable electrons allows the metal to conduct electric current. When an electrical potential difference (a voltage) is applied across the metal, the resulting electric field causes electrons to drift towards the positive terminal. The actual drift velocity of electrons is typically small, on the order of magnitude of meters per hour. However, due to the sheer number of moving electrons, even a slow drift velocity results in a large current density.^[10] The mechanism is similar to transfer of momentum of balls in a Newton's cradle^[11] but the rapid propagation of an electric energy along a wire is not due to the mechanical forces, but the propagation of an energy-carrying electromagnetic field guided by the wire.

Most metals have electrical resistance. In simpler models (non quantum mechanical models) this can be explained by replacing electrons and the crystal lattice by a wave-like structure. When the electron wave travels through the lattice, the waves interfere, which causes resistance. The more regular the lattice is, the less disturbance happens and thus the less resistance. The amount of resistance is thus mainly caused by two factors. First, it is caused by the temperature and thus amount of vibration of the crystal lattice. The temperature causes bigger vibrations, which act as irregularities in the lattice. Second, the purity of the metal is relevant as a mixture of different ions is also an irregularity.^[12]^[13]

In semiconductors and insulators

In metals, the Fermi level lies in the conduction band (see Band Theory, above) giving rise to free conduction electrons. However, in semiconductors the position of the Fermi level is within the band gap, about halfway between the conduction band minimum (the bottom of the first band of unfilled electron energy levels) and the valence band maximum (the top of the band below the conduction band, of filled electron energy levels). That applies for intrinsic (undoped) semiconductors. This means that at absolute zero temperature, there would be no free conduction electrons, and the resistance is infinite. However, the resistance decreases as the charge carrier density (i.e., without introducing further complications, the density of electrons) in the conduction band increases. In extrinsic (doped) semiconductors, dopant atoms increase the majority charge carrier concentration by donating electrons to the conduction band or producing holes in the valence band. (A "hole" is a position where an electron is missing; such holes can behave in a similar way to electrons.) For both types of donor or acceptor atoms, increasing dopant density reduces resistance. Hence, highly doped semiconductors behave metallically. At very high temperatures, the contribution of thermally generated carriers dominates over the contribution from dopant atoms, and the resistance decreases exponentially with temperature.

In ionic liquids/electrolytes

In electrolytes, electrical conduction happens not by band electrons or holes, but by full atomic species (ions) traveling, each carrying an electrical charge. The resistivity of ionic solutions (electrolytes) varies tremendously with concentration – while distilled water is almost an insulator, salt water is a reasonable electrical conductor. Conduction in ionic liquids is also controlled by the movement of ions, but here we are talking about molten salts rather than solvated ions. In biological membranes, currents are carried by ionic salts. Small holes in cell membranes, called ion channels, are selective to specific ions and determine the membrane resistance.

Superconductivity

The electrical resistivity of a metallic conductor decreases gradually as temperature is lowered. In ordinary conductors, such as copper or silver, this decrease is limited by impurities and other defects. Even near absolute zero, a real sample of a normal conductor shows some resistance. In a superconductor, the resistance drops abruptly to zero when the material is cooled below its critical temperature. An electric current flowing in a loop of superconducting wire can persist indefinitely with no power source.^[14]

In 1986, researchers discovered that some cuprate-perovskite ceramic materials have much higher critical temperatures, and in 1987 one was produced with a critical temperature above 90 K (−183 °C).^[15] Such a high transition temperature is theoretically impossible for a conventional superconductor, so the researchers named these conductors high-temperature superconductors. Liquid nitrogen boils at 77 K, cold enough to activate high-temperature superconductors, but not nearly cold enough for conventional superconductors. In conventional superconductors, electrons are held together in pairs by an attraction mediated by lattice phonons.^{[clarification needed]} The best available model of high-temperature superconductivity is still somewhat crude. There is a hypothesis that electron pairing in high-temperature superconductors is mediated by short-range spin waves known as paramagnons.^[16]^{[dubious – discuss]}

Plasma

Lightning is an example of plasma present at Earth's surface. Typically, lightning discharges 30,000 amperes at up to 100 million volts, and emits light, radio waves, and X-rays.^[17] Plasma temperatures in lightning might approach 30,000 Kelvin (29,727 °C) (53,540 °F), or five times hotter than the temperature at the sun surface, and electron densities may exceed 10²⁴ m⁻³.

Plasmas are very good conductors and electric potentials play an important role.

The potential as it exists on average in the space between charged particles, independent of the question of how it can be measured, is called the plasma potential, or space potential. If an electrode is inserted into a plasma, its potential generally lies considerably below the plasma potential, due to what is termed a Debye sheath. The good electrical conductivity of plasmas makes their electric fields very small. This results in the important concept of quasineutrality, which says the density of negative charges is approximately equal to the density of positive charges over large volumes of the plasma (n_e = <Z>n_i), but on the scale of the Debye length there can be charge imbalance. In the special case that double layers are formed, the charge separation can extend some tens of Debye lengths.

The magnitude of the potentials and electric fields must be determined by means other than simply finding the net charge density. A common example is to assume that the electrons satisfy the Boltzmann relation:

displaystyle n_textepropto e^ePhi /k_textBT_texte.

Differentiating this relation provides a means to calculate the electric field from the density:

displaystyle mathbf E =-frac k_textBT_texteefrac nabla n_texten_texte.

(The "downward pointing triangle" is a vector gradient; see nabla symbol and gradient for more information.)

It is possible to produce a plasma that is not quasineutral. An electron beam, for example, has only negative charges. The density of a non-neutral plasma must generally be very low, or it must be very small. Otherwise, the repulsive electrostatic force dissipates it.

In astrophysical plasmas, Debye screening prevents electric fields from directly affecting the plasma over large distances, i.e., greater than the Debye length. However, the existence of charged particles causes the plasma to generate, and be affected by, magnetic fields. This can and does cause extremely complex behavior, such as the generation of plasma double layers, an object that separates charge over a few tens of Debye lengths. The dynamics of plasmas interacting with external and self-generated magnetic fields are studied in the academic discipline of magnetohydrodynamics.

Plasma is often called the fourth state of matter after solid, liquids and gases.^[18]^[19] It is distinct from these and other lower-energy states of matter. Although it is closely related to the gas phase in that it also has no definite form or volume, it differs in a number of ways, including the following:

Property	Gas	Plasma
Electrical conductivity	Very low: air is an excellent insulator until it breaks down into plasma at electric field strengths above 30 kilovolts per centimeter.^[20]	Usually very high: for many purposes, the conductivity of a plasma may be treated as infinite.
Independently acting species	One: all gas particles behave in a similar way, influenced by gravity and by collisions with one another.	Two or three: electrons, ions, protons and neutrons can be distinguished by the sign and value of their charge so that they behave independently in many circumstances, with different bulk velocities and temperatures, allowing phenomena such as new types of waves and instabilities.
Velocity distribution	Maxwellian: collisions usually lead to a Maxwellian velocity distribution of all gas particles, with very few relatively fast particles.	Often non-Maxwellian: collisional interactions are often weak in hot plasmas and external forcing can drive the plasma far from local equilibrium and lead to a significant population of unusually fast particles.
Interactions	Binary: two-particle collisions are the rule, three-body collisions extremely rare.	Collective: waves, or organized motion of plasma, are very important because the particles can interact at long ranges through the electric and magnetic forces.

Resistivity and conductivity of various materials

A conductor such as a metal has high conductivity and a low resistivity.

An insulator like glass has low conductivity and a high resistivity.

The conductivity of a semiconductor is generally intermediate, but varies widely under different conditions, such as exposure of the material to electric fields or specific frequencies of light, and, most important, with temperature and composition of the semiconductor material.

The degree of doping in semiconductors makes a large difference in conductivity. To a point, more doping leads to higher conductivity. The conductivity of a solution of water is highly dependent on its concentration of dissolved salts, and other chemical species that ionize in the solution. Electrical conductivity of water samples is used as an indicator of how salt-free, ion-free, or impurity-free the sample is; the purer the water, the lower the conductivity (the higher the resistivity). Conductivity measurements in water are often reported as specific conductance, relative to the conductivity of pure water at 7002298150000000000♠25 °C. An EC meter is normally used to measure conductivity in a solution. A rough summary is as follows:

Material	Resistivity, ρ (Ω·m)
Superconductors	0
Metals	10⁻⁸
Semiconductors	Variable
Electrolytes	Variable
Insulators	10¹⁶
Superinsulators	∞

This table shows the resistivity (ρ), conductivity and temperature coefficient of various materials at 20 °C (68 °F, 293 K)

Material	Resistivity ρ (Ω·m) at 7002293150000000000♠20 °C	Conductivity σ (S/m) at 7002293150000000000♠20 °C	Temperature coefficient^[a] (K⁻¹)	Reference
Silver	6992159000000000000♠1.59×10⁻⁸	7007630000000000000♠6.30×10⁷	0.0038	^[21]^[22]
Copper	6992167999999999999♠1.68×10⁻⁸	7007596000000000000♠5.96×10⁷	0.00404	^[23]^[24]
Annealed copper^[b]	6992172000000000000♠1.72×10⁻⁸	7007580000000000000♠5.80×10⁷	0.00393	^[25]
Gold^[c]	6992244000000000000♠2.44×10⁻⁸	7007410000000000000♠4.1×10⁷	0.0034	^[21]
Aluminium^[d]	6992265000000000000♠2.65×10⁻⁸	7007377000000000000♠3.77×10⁷	0.0039	^[21]
Calcium	6992335999999999999♠3.36×10⁻⁸	7007298000000000000♠2.98×10⁷	0.0041
Tungsten	6992560000000000000♠5.60×10⁻⁸	7007179000000000000♠1.79×10⁷	0.0045	^[21]
Zinc	6992590000000000000♠5.90×10⁻⁸	7007169000000000000♠1.69×10⁷	0.0037	^[26]
Nickel	6992699000000000000♠6.99×10⁻⁸	7007143000000000000♠1.43×10⁷	0.006
Lithium	6992928000000000000♠9.28×10⁻⁸	7007108000000000000♠1.08×10⁷	0.006
Iron	6992970000000000000♠9.7×10⁻⁸	7007100000000000000♠1×10⁷	0.005	^[21]
Platinum	6993106000000000000♠1.06×10⁻⁷	7006943000000000000♠9.43×10⁶	0.00392	^[21]
Tin	6993109000000000000♠1.09×10⁻⁷	7006917000000000000♠9.17×10⁶	0.0045
Gallium	6993139999999999999♠1.40×10⁻⁷	7006710000000000000♠7.1×10⁶	0.004
Niobium	6993139999999999999♠1.4×10⁻⁷	7006700000000000000♠7×10⁶		^[27]
Carbon steel (1010)	6993143000000000000♠1.43×10⁻⁷	7006699000000000000♠6.99×10⁶		^[28]
Lead	6993220000000000000♠2.20×10⁻⁷	7006455000000000000♠4.55×10⁶	0.0039	^[21]
Titanium	6993420000000000000♠4.20×10⁻⁷	7006238000000000000♠2.38×10⁶	0.0038
Grain oriented electrical steel	6993459999999999999♠4.60×10⁻⁷	7006217000000000000♠2.17×10⁶		^[29]
Manganin	6993482000000000000♠4.82×10⁻⁷	7006206999999999999♠2.07×10⁶	0.000002	^[30]
Constantan	6993489999999999999♠4.90×10⁻⁷	7006204000000000000♠2.04×10⁶	0.000008	^[31]
Stainless steel^[e]	6993690000000000000♠6.90×10⁻⁷	7006145000000000000♠1.45×10⁶	0.00094	^[32]
Mercury	6993979999999999999♠9.80×10⁻⁷	7006102000000000000♠1.02×10⁶	0.0009	^[30]
Manganese	6994144000000000000♠1.44×10⁻⁶	7005694000000000000♠6.94×10⁵
Nichrome^[f]	6994110000000000000♠1.10×10⁻⁶	7005670000000000000♠6.7×10⁵ ^{[citation needed]}	6996400000000000000♠0.0004	^[21]
Carbon (amorphous)	6996500000000000000♠5×10⁻⁴ to 6996800000000000000♠8×10⁻⁴	7003125000000000000♠1.25×10³ to 7003200000000000000♠2×10³	−0.0005	^[21]^[33]
Carbon (graphite) parallel to basal plane^[g]	6994249999999999999♠2.5×10⁻⁶ to 6994499999999999999♠5×10⁻⁶	7005200000000000000♠2×10⁵ to 7005300000000000000♠3.00×10⁵ ^{[citation needed]}		^[4]
Carbon (graphite) perpendicular to basal plane^[h]	6997300000000000000♠3.0×10⁻³	7002330000000000000♠3.3×10²		^[4]
GaAs	6997100000000000000♠1.00×10⁻³ to 7008100000000000000♠1×10⁸	6992100000000000000♠1.00×10⁻⁸ to 7003100000000000000♠10³		^[34]
Germanium^[i]	6999459999999999999♠4.6×10⁻¹	2.17	−0.048	^[21]^[22]
Sea water^[j]	6999200000000000000♠2.00×10⁻¹	7000480000000000000♠4.8		^[35]
Swimming pool water^[k]	6999330000000000000♠3.3×10⁻¹ to 6999400000000000000♠4.00×10⁻¹	6999250000000000000♠0.25 to 6999300000000000000♠0.30		^[36]
Drinking water^[l]	7001200000000000000♠2×10¹ to 7003200000000000000♠2×10³	6996500000000000000♠5×10⁻⁴ to 6998500000000000000♠5×10⁻²		^{[citation needed]}
Silicon^[i]	7002640000000000000♠6.4×10²	6997156000000000000♠1.56×10⁻³	3001250000000000000♠−0.075	^[21]
Wood (damp)	7003100000000000000♠1×10³ to 7004100000000000000♠1×10⁴	6996100000000000000♠10⁻⁴ to 6997100000000000000♠10⁻³		^[37]
Deionized water^[m]	7005180000000000000♠1.80×10⁵	6994550000000000000♠5.50×10⁻⁶		^[38]
Glass	7011100000000000000♠1×10¹¹ to 7015100000000000000♠1×10¹⁵	6985100000000000000♠10⁻¹⁵ to 6989100000000000000♠10⁻¹¹	?	^[21]^[22]
Carbon (diamond)	7012100000000000000♠1×10¹²	~6987100000000000000♠10⁻¹³		^[39]
Hard rubber	7013100000000000000♠1×10¹³	6986100000000000000♠10⁻¹⁴	?	^[21]
Air	7009100000000000000♠10⁹ to 7015100000000000000♠10¹⁵	~6985100000000000000♠10⁻¹⁵ to 6991100000000000000♠10⁻⁹		^[40]^[41]
Wood (oven dry)	7014100000000000000♠1×10¹⁴ to 7016100000000000000♠1×10¹⁶	6984100000000000000♠10⁻¹⁶ to 6986100000000000000♠10⁻¹⁴		^[37]
Sulfur	7015100000000000000♠1×10¹⁵	6984100000000000000♠10⁻¹⁶	?	^[21]
Fused quartz	7017750000000000000♠7.5×10¹⁷	6982130000000000000♠1.3×10⁻¹⁸	?	^[21]
PET	7021100000000000000♠1×10²¹	6979099999999999999♠10⁻²¹	?
Teflon	7023100000000000000♠1×10²³ to 7025100000000000000♠1×10²⁵	6975100000000000000♠10⁻²⁵ to 6977099999999999999♠10⁻²³	?

The effective temperature coefficient varies with temperature and purity level of the material. The 20 °C value is only an approximation when used at other temperatures. For example, the coefficient becomes lower at higher temperatures for copper, and the value 0.00427 is commonly specified at 7002273149999999999♠0 °C.^[42]

The extremely low resistivity (high conductivity) of silver is characteristic of metals. George Gamow tidily summed up the nature of the metals' dealings with electrons in his popular science book One, Two, Three...Infinity (1947):

.mw-parser-output .templatequoteoverflow:hidden;margin:1em 0;padding:0 40px.mw-parser-output .templatequote .templatequoteciteline-height:1.5em;text-align:left;padding-left:1.6em;margin-top:0

The metallic substances differ from all other materials by the fact that the outer shells of their atoms are bound rather loosely, and often let one of their electrons go free. Thus the interior of a metal is filled up with a large number of unattached electrons that travel aimlessly around like a crowd of displaced persons. When a metal wire is subjected to electric force applied on its opposite ends, these free electrons rush in the direction of the force, thus forming what we call an electric current.

More technically, the free electron model gives a basic description of electron flow in metals.

Wood is widely regarded as an extremely good insulator, but its resistivity is sensitively dependent on moisture content, with damp wood being a factor of at least 7010100000000000000♠10¹⁰ worse insulator than oven-dry.^[37] In any case, a sufficiently high voltage – such as that in lightning strikes or some high-tension powerlines – can lead to insulation breakdown and electrocution risk even with apparently dry wood.

Temperature dependence

Linear approximation

The electrical resistivity of most materials changes with temperature. If the temperature T does not vary too much, a linear approximation is typically used:

rho (T)=rho _0[1+alpha (T-T_0)]

where $alpha$ is called the temperature coefficient of resistivity, $T_0$ is a fixed reference temperature (usually room temperature), and $rho _0$ is the resistivity at temperature $T_0$ . The parameter $alpha$ is an empirical parameter fitted from measurement data. Because the linear approximation is only an approximation, $alpha$ is different for different reference temperatures. For this reason it is usual to specify the temperature that $alpha$ was measured at with a suffix, such as $alpha _15$ , and the relationship only holds in a range of temperatures around the reference.^[43] When the temperature varies over a large temperature range, the linear approximation is inadequate and a more detailed analysis and understanding should be used.

Metals

Temperature dependence of the resistivity of gold, copper and silver.

In general, electrical resistivity of metals increases with temperature. Electron–phonon interactions can play a key role. At high temperatures, the resistance of a metal increases linearly with temperature. As the temperature of a metal is reduced, the temperature dependence of resistivity follows a power law function of temperature. Mathematically the temperature dependence of the resistivity ρ of a metal is given by the Bloch–Grüneisen formula:

rho (T)=rho (0)+Aleft(frac TTheta _Rright)^nint _0^frac Theta _RTfrac x^n(e^x-1)(1-e^-x)dx

where $rho (0)$ is the residual resistivity due to defect scattering, A is a constant that depends on the velocity of electrons at the Fermi surface, the Debye radius and the number density of electrons in the metal. $Theta _R$ is the Debye temperature as obtained from resistivity measurements and matches very closely with the values of Debye temperature obtained from specific heat measurements. n is an integer that depends upon the nature of interaction:

n=5 implies that the resistance is due to scattering of electrons by phonons (as it is for simple metals)

n=3 implies that the resistance is due to s-d electron scattering (as is the case for transition metals)

n=2 implies that the resistance is due to electron–electron interaction.

If more than one source of scattering is simultaneously present, Matthiessen's Rule (first formulated by Augustus Matthiessen in the 1860s)^[44]^[45] states that the total resistance can be approximated by adding up several different terms, each with the appropriate value of n.

As the temperature of the metal is sufficiently reduced (so as to 'freeze' all the phonons), the resistivity usually reaches a constant value, known as the residual resistivity. This value depends not only on the type of metal, but on its purity and thermal history. The value of the residual resistivity of a metal is decided by its impurity concentration. Some materials lose all electrical resistivity at sufficiently low temperatures, due to an effect known as superconductivity.

An investigation of the low-temperature resistivity of metals was the motivation to Heike Kamerlingh Onnes's experiments that led in 1911 to discovery of superconductivity. For details see History of superconductivity.

Semiconductors

In general, intrinsic semiconductor resistivity decreases with increasing temperature. The electrons are bumped to the conduction energy band by thermal energy, where they flow freely, and in doing so leave behind holes in the valence band, which also flow freely. The electric resistance of a typical intrinsic (non doped) semiconductor decreases exponentially with temperature:

rho =rho _0e^-aT,

An even better approximation of the temperature dependence of the resistivity of a semiconductor is given by the Steinhart–Hart equation:

displaystyle frac 1T=A+Bln(rho )+C(ln(rho ))^3,

where A, B and C are the so-called Steinhart–Hart coefficients.

This equation is used to calibrate thermistors.

Extrinsic (doped) semiconductors have a far more complicated temperature profile. As temperature increases starting from absolute zero they first decrease steeply in resistance as the carriers leave the donors or acceptors. After most of the donors or acceptors have lost their carriers, the resistance starts to increase again slightly due to the reducing mobility of carriers (much as in a metal). At higher temperatures, they behave like intrinsic semiconductors as the carriers from the donors/acceptors become insignificant compared to the thermally generated carriers.^[46]

In non-crystalline semiconductors, conduction can occur by charges quantum tunnelling from one localised site to another. This is known as variable range hopping and has the characteristic form of

displaystyle rho =Aexp left(T^-frac 1nright)

,

where n = 2, 3, 4, depending on the dimensionality of the system.

Complex resistivity and conductivity

When analyzing the response of materials to alternating electric fields (dielectric spectroscopy),^[47] in applications such as electrical impedance tomography,^[48] it is convenient to replace resistivity with a complex quantity called impedivity (in analogy to electrical impedance). Impedivity is the sum of a real component, the resistivity, and an imaginary component, the reactivity (in analogy to reactance). The magnitude of impedivity is the square root of sum of squares of magnitudes of resistivity and reactivity.

Conversely, in such cases the conductivity must be expressed as a complex number (or even as a matrix of complex numbers, in the case of anisotropic materials) called the admittivity. Admittivity is the sum of a real component called the conductivity and an imaginary component called the susceptivity.

An alternative description of the response to alternating currents uses a real (but frequency-dependent) conductivity, along with a real permittivity. The larger the conductivity is, the more quickly the alternating-current signal is absorbed by the material (i.e., the more opaque the material is). For details, see Mathematical descriptions of opacity.

Resistance versus resistivity in complicated geometries

Even if the material's resistivity is known, calculating the resistance of something made from it may, in some cases, be much more complicated than the formula $R=rho ell /A$ above. One example is spreading resistance profiling, where the material is inhomogeneous (different resistivity in different places), and the exact paths of current flow are not obvious.

In cases like this, the formulas

J=sigma E,,rightleftharpoons ,,E=rho J,!

must be replaced with

mathbf J (mathbf r )=sigma (mathbf r )mathbf E (mathbf r ),,rightleftharpoons ,,mathbf E (mathbf r )=rho (mathbf r )mathbf J (mathbf r ),,!

where E and J are now vector fields. This equation, along with the continuity equation for J and the Poisson's equation for E, form a set of partial differential equations. In special cases, an exact or approximate solution to these equations can be worked out by hand, but for very accurate answers in complex cases, computer methods like finite element analysis may be required.

Resistivity density products

In some applications where the weight of an item is very important, resistivity density products are more important than absolute low resistivity – it is often possible to make the conductor thicker to make up for a higher resistivity; and then a low resistivity density product material (or equivalently a high conductivity to density ratio) is desirable. For example, for long distance overhead power lines, aluminium is frequently used rather than copper (Cu) because it is lighter for the same conductance.

Silver, although it is the least resistive metal known, has a high density and performs similarly to copper by this measure, but is much more expensive. Calcium and the alkali metals have the best resistivity-density products, but are rarely used for conductors due to their high reactivity with water and oxygen (and lack of physical strength). Aluminium is far more stable. Two other important attributes, price and toxicity, exclude the (otherwise) best choice^{[citation needed]}: beryllium. (Pure beryllium is also brittle.) Thus, aluminium is usually the metal of choice when the weight or cost of a conductor is the driving consideration.

Material	Resistivity (nΩ·m)	Density (g/cm³)	Resistivity × density product		Relative volume required to give same conductance as Cu	Relative weight (mass) required to give same conductance as Cu	Approx price (USD per kg) (12/9/2018)	Relative cost versus Cu
Material	Resistivity (nΩ·m)	Density (g/cm³)	(g.Ω.m⁻¹)	Relative to Cu	Relative volume required to give same conductance as Cu		Approx price (USD per kg) (12/9/2018)	Relative cost versus Cu
Sodium	47.7	0.97	46	31%	2.843	0.31
Lithium	92.8	0.53	49	33%	5.531	0.33
Calcium	33.6	1.55	52	35%	2.002	0.35
Potassium	72.0	0.89	64	43%	4.291	0.43
Beryllium	35.6	1.85	66	44%	2.122	0.44
Aluminium	26.50	2.70	72	48%	1.5792	0.48	2.0	0.16
Magnesium	43.90	1.74	76	51%	2.616	0.51
Copper	16.78	8.96	150	100%	1	1	6.0	1
Silver	15.87	10.49	166	111%	0.946	1.11	456	84
Gold	22.14	19.30	427	285%	1.319	2.85	39,000	19,000
Iron	96.1	7.874	757	505%	5.727	5.05

Notes

^ The numbers in this column increase or decrease the significand portion of the resistivity. For example, at 30 °C (303 K), the resistivity of silver is 6992165000000000000♠1.65×10⁻⁸. This is calculated as Δρ = α ΔT ρ_o where ρ_o is the resistivity at 7002293150000000000♠20 °C (in this case) and α is the temperature coefficient.

^ Referred to as 100% IACS or International Annealed Copper Standard. The unit for expressing the conductivity of nonmagnetic materials by testing using the eddy-current method. Generally used for temper and alloy verification of aluminium.

^ Gold is commonly used in electrical contacts because it does not easily corrode.

^ Commonly used for high voltage power lines

^ 18% chromium and 8% nickel austenitic stainless steel

^ Nickel-iron-chromium alloy commonly used in heating elements.

^ Graphite is strongly anisotropic.

^ Graphite is strongly anisotropic.

^ ^a^b The resistivity of semiconductors depends strongly on the presence of impurities in the material.

^ Corresponds to an average salinity of 35 g/kg at 7002293150000000000♠20 °C.

^ The pH should be around 8.4 and the conductivity in the range of 2.5–3 mS/cm. The lower value is appropriate for freshly prepared water. The conductivity is used for the determination of TDS (total dissolved particles).

^ This value range is typical of high quality drinking water and not an indicator of water quality

^ Conductivity is lowest with monatomic gases present; changes to 6996120000000000000♠1.2×10⁻⁴ upon complete de-gassing, or to 6995750000000000000♠7.5×10⁻⁵ upon equilibration to the atmosphere due to dissolved CO₂

References

^ Lowrie (2007-09-20). Fundamentals of Geophysics. Cambridge University Press. pp. 254–. ISBN 978-1-139-46595-3..mw-parser-output cite.citationfont-style:inherit.mw-parser-output qquotes:"""""""'""'".mw-parser-output code.cs1-codecolor:inherit;background:inherit;border:inherit;padding:inherit.mw-parser-output .cs1-lock-free abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-lock-subscription abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registrationcolor:#555.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration spanborder-bottom:1px dotted;cursor:help.mw-parser-output .cs1-hidden-errordisplay:none;font-size:100%.mw-parser-output .cs1-visible-errorfont-size:100%.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-formatfont-size:95%.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-leftpadding-left:0.2em.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-rightpadding-right:0.2em

^ Narinder Kumar (2003). Comprehensive Physics XII. Laxmi Publications. pp. 282–. ISBN 978-81-7008-592-8.

^ Eric Bogatin (2004). Signal Integrity: Simplified. Prentice Hall Professional. pp. 114–. ISBN 978-0-13-066946-9.

^ ^a^b^c Hugh O. Pierson, Handbook of carbon, graphite, diamond, and fullerenes: properties, processing, and applications, p. 61, William Andrew, 1993
ISBN 0-8155-1339-9.

^ J.R. Tyldesley (1975) An introduction to Tensor Analysis: For Engineers and Applied Scientists, Longman,
ISBN 0-582-44355-5

^ G. Woan (2010) The Cambridge Handbook of Physics Formulas, Cambridge University Press,
ISBN 978-0-521-57507-2

^ Josef Pek, Tomas Verner (3 Apr 2007). "Finite‐difference modelling of magnetotelluric fields in two‐dimensional anisotropic media". Geophysical Journal International. 128 (3): 505–521. doi:10.1111/j.1365-246X.1997.tb05314.x.

^ David Tong (Jan 2016). "The Quantum Hall Effect: TIFR Infosys Lectures" (PDF). Retrieved 14 Sep 2018.

^ Bonding (sl). ibchem.com

^ "Current versus Drift Speed". The physics classroom. Retrieved 20 August 2014.

^ Lowe, Doug (2012). Electronics All-in-One For Dummies. John Wiley & Sons. ISBN 978-0-470-14704-7.

^ Keith Welch. "Questions & Answers - How do you explain electrical resistance?". Thomas Jefferson National Accelerator Facility. Retrieved 28 April 2017.

^ "Electromigration : What is electromigration?". Middle East Technical University. Retrieved 31 July 2017. When electrons are conducted through a metal, they interact with imperfections in the lattice and scatter. […] Thermal energy produces scattering by causing atoms to vibrate. This is the source of resistance of metals.

^
John C. Gallop (1990). SQUIDS, the Josephson Effects and Superconducting Electronics. CRC Press. pp. 3, 20. ISBN 978-0-7503-0051-3.

^ "The History of Superconductors". Archived from the original on 3 March 2016. Retrieved 23 February 2016.

^ D. Pines (2002). "The Spin Fluctuation Model for High Temperature Superconductivity: Progress and Prospects". The Gap Symmetry and Fluctuations in High-Tc Superconductors. NATO Science Series: B:. 371. New York: Kluwer Academic. pp. 111–142. doi:10.1007/0-306-47081-0_7. ISBN 978-0-306-45934-4.

^ See Flashes in the Sky: Earth's Gamma-Ray Bursts Triggered by Lightning

^ Yaffa Eliezer, Shalom Eliezer, The Fourth State of Matter: An Introduction to the Physics of Plasma, Publisher: Adam Hilger, 1989,
ISBN 978-0-85274-164-1, 226 pages, page 5

^ Bittencourt, J.A. (2004). Fundamentals of Plasma Physics. Springer. p. 1. ISBN 9780387209753.

^ Hong, Alice (2000). "Dielectric Strength of Air". The Physics Factbook.

^ ^a^b^c^d^e^f^g^hⁱ^j^k^l^mⁿ^o Raymond A. Serway (1998). Principles of Physics (2nd ed.). Fort Worth, Texas; London: Saunders College Pub. p. 602. ISBN 978-0-03-020457-9.

^ ^a^b^c David Griffiths (1999) [1981]. "7. Electrodynamics". In Alison Reeves. Introduction to Electrodynamics (3rd ed.). Upper Saddle River, New Jersey: Prentice Hall. p. 286. ISBN 978-0-13-805326-0. OCLC 40251748.

^ Matula, R.A. (1979). "Electrical resistivity of copper, gold, palladium, and silver". Journal of Physical and Chemical Reference Data. 8 (4): 1147. Bibcode:1979JPCRD...8.1147M. doi:10.1063/1.555614.

^ Douglas Giancoli (2009) [1984]. "25. Electric Currents and Resistance". In Jocelyn Phillips. Physics for Scientists and Engineers with Modern Physics (4th ed.). Upper Saddle River, New Jersey: Prentice Hall. p. 658. ISBN 978-0-13-149508-1.

^ Copper wire tables : United States. National Bureau of Standards : Free Download & Streaming : Internet Archive. Archive.org (2001-03-10). Retrieved on 2014-02-03.

^ Physical constants. (PDF format; see page 2, table in the right lower corner). Retrieved on 2011-12-17.

^
Material properties of niobium.

^ AISI 1010 Steel, cold drawn. Matweb

^ "JFE steel" (PDF). Retrieved 2012-10-20.

^ ^a^b Douglas C. Giancoli (1995). Physics: Principles with Applications (4th ed.). London: Prentice Hall. ISBN 978-0-13-102153-2.

(see also Table of Resistivity. hyperphysics.phy-astr.gsu.edu)

^ John O'Malley (1992) Schaum's outline of theory and problems of basic circuit analysis, p. 19, McGraw-Hill Professional,
ISBN 0-07-047824-4

^ Glenn Elert (ed.), "Resistivity of steel", The Physics Factbook, retrieved and archived 16 June 2011.

^ Y. Pauleau, Péter B. Barna, P. B. Barna (1997) Protective coatings and thin films: synthesis, characterization, and applications, p. 215, Springer,
ISBN 0-7923-4380-8.

^ Milton Ohring (1995). Engineering materials science, Volume 1 (3rd ed.). Academic Press. p. 561. ISBN 978-0125249959.

^ Physical properties of sea water. Kayelaby.npl.co.uk. Retrieved on 2011-12-17.

^ [1]. chemistry.stackexchange.com

^ ^a^b^c Transmission Lines data. Transmission-line.net. Retrieved on 2014-02-03.

^ R. M. Pashley; M. Rzechowicz; L. R. Pashley; M. J. Francis (2005). "De-Gassed Water is a Better Cleaning Agent". The Journal of Physical Chemistry B. 109 (3): 1231–8. doi:10.1021/jp045975a. PMID 16851085.

^ Lawrence S. Pan, Don R. Kania, Diamond: electronic properties and applications, p. 140, Springer, 1994
ISBN 0-7923-9524-7.

^ S. D. Pawar; P. Murugavel; D. M. Lal (2009). "Effect of relative humidity and sea level pressure on electrical conductivity of air over Indian Ocean". Journal of Geophysical Research. 114: D02205. Bibcode:2009JGRD..11402205P. doi:10.1029/2007JD009716.

^ E. Seran; M. Godefroy; E. Pili (2016). "What we can learn from measurements of air electric conductivity in 222Rn ‐ rich atmosphere". Earth and Space Science. 4 (2): 91–106. Bibcode:2017E&SS....4...91S. doi:10.1002/2016EA000241.

^ Copper Wire Tables. US Dep. of Commerce. National Bureau of Standards Handbook. February 21, 1966

^ M.R. Ward (1971) Electrical Engineering Science, pp. 36–40, McGraw-Hill.

^ A. Matthiessen, Rep. Brit. Ass. 32, 144 (1862)

^ A. Matthiessen, Progg. Anallen, 122, 47 (1864)

^ J. Seymour (1972) Physical Electronics, chapter 2, Pitman

^ Stephenson, C.; Hubler, A. (2015). "Stability and conductivity of self-assembled wires in a transverse electric field". Sci. Rep. 5: 15044. Bibcode:2015NatSR...515044S. doi:10.1038/srep15044. PMC 4604515. PMID 26463476.

^ Otto H. Schmitt, University of Minnesota Mutual Impedivity Spectrometry and the Feasibility of its Incorporation into Tissue-Diagnostic Anatomical Reconstruction and Multivariate Time-Coherent Physiological Measurements. otto-schmitt.org. Retrieved on 2011-12-17.

External links

"Electrical Conductivity". Sixty Symbols. Brady Haran for the University of Nottingham. 2010.

Electrical Resistivity and conductivity-Wikipedia article spoken for the blind "Audiopedia as of July 17, 2014"

Comparison of the electrical conductivity of various elements in WolframAlpha

[21] The numbers in this column increase or decrease the significand portion of the resistivity. For example, at 30 °C (303 K), the resistivity of silver is 6992165000000000000♠1.65×10⁻⁸. This is calculated as Δρ = α ΔT ρ_o where ρ_o is the resistivity at 7002293150000000000♠20 °C (in this case) and α is the temperature coefficient.

[26] Referred to as 100% IACS or International Annealed Copper Standard. The unit for expressing the conductivity of nonmagnetic materials by testing using the eddy-current method. Generally used for temper and alloy verification of aluminium.

[28] Gold is commonly used in electrical contacts because it does not easily corrode.

[29] Commonly used for high voltage power lines

[36] 18% chromium and 8% nickel austenitic stainless steel

[38] Nickel-iron-chromium alloy commonly used in heating elements.

[40] Graphite is strongly anisotropic.

[41] Graphite is strongly anisotropic.

[semi-43] The resistivity of semiconductors depends strongly on the presence of impurities in the material.

[44] Corresponds to an average salinity of 35 g/kg at 7002293150000000000♠20 °C.

[46] The pH should be around 8.4 and the conductivity in the range of 2.5–3 mS/cm. The lower value is appropriate for freshly prepared water. The conductivity is used for the determination of TDS (total dissolved particles).

[48] This value range is typical of high quality drinking water and not an indicator of water quality

[50] Conductivity is lowest with monatomic gases present; changes to 6996120000000000000♠1.2×10⁻⁴ upon complete de-gassing, or to 6995750000000000000♠7.5×10⁻⁵ upon equilibration to the atmosphere due to dissolved CO₂

[1] Lowrie (2007-09-20). Fundamentals of Geophysics. Cambridge University Press. pp. 254–. ISBN 978-1-139-46595-3..mw-parser-output cite.citationfont-style:inherit.mw-parser-output qquotes:"""""""'""'".mw-parser-output code.cs1-codecolor:inherit;background:inherit;border:inherit;padding:inherit.mw-parser-output .cs1-lock-free abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-lock-subscription abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registrationcolor:#555.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration spanborder-bottom:1px dotted;cursor:help.mw-parser-output .cs1-hidden-errordisplay:none;font-size:100%.mw-parser-output .cs1-visible-errorfont-size:100%.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-formatfont-size:95%.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-leftpadding-left:0.2em.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-rightpadding-right:0.2em

[2] Narinder Kumar (2003). Comprehensive Physics XII. Laxmi Publications. pp. 282–. ISBN 978-81-7008-592-8.

[3] Eric Bogatin (2004). Signal Integrity: Simplified. Prentice Hall Professional. pp. 114–. ISBN 978-0-13-066946-9.

[Pierson-4] Hugh O. Pierson, Handbook of carbon, graphite, diamond, and fullerenes: properties, processing, and applications, p. 61, William Andrew, 1993
ISBN 0-8155-1339-9.

[5] J.R. Tyldesley (1975) An introduction to Tensor Analysis: For Engineers and Applied Scientists, Longman,
ISBN 0-582-44355-5

[6] G. Woan (2010) The Cambridge Handbook of Physics Formulas, Cambridge University Press,
ISBN 978-0-521-57507-2

[7] Josef Pek, Tomas Verner (3 Apr 2007). "Finite‐difference modelling of magnetotelluric fields in two‐dimensional anisotropic media". Geophysical Journal International. 128 (3): 505–521. doi:10.1111/j.1365-246X.1997.tb05314.x.

[8] David Tong (Jan 2016). "The Quantum Hall Effect: TIFR Infosys Lectures" (PDF). Retrieved 14 Sep 2018.

[9] Bonding (sl). ibchem.com

[classroom-10] "Current versus Drift Speed". The physics classroom. Retrieved 20 August 2014.

[11] Lowe, Doug (2012). Electronics All-in-One For Dummies. John Wiley & Sons. ISBN 978-0-470-14704-7.

[12] Keith Welch. "Questions & Answers - How do you explain electrical resistance?". Thomas Jefferson National Accelerator Facility. Retrieved 28 April 2017.

[13] "Electromigration : What is electromigration?". Middle East Technical University. Retrieved 31 July 2017. When electrons are conducted through a metal, they interact with imperfections in the lattice and scatter. […] Thermal energy produces scattering by causing atoms to vibrate. This is the source of resistance of metals.

[Gallop-14] 
John C. Gallop (1990). SQUIDS, the Josephson Effects and Superconducting Electronics. CRC Press. pp. 3, 20. ISBN 978-0-7503-0051-3.

[15] "The History of Superconductors". Archived from the original on 3 March 2016. Retrieved 23 February 2016.

[16] D. Pines (2002). "The Spin Fluctuation Model for High Temperature Superconductivity: Progress and Prospects". The Gap Symmetry and Fluctuations in High-Tc Superconductors. NATO Science Series: B:. 371. New York: Kluwer Academic. pp. 111–142. doi:10.1007/0-306-47081-0_7. ISBN 978-0-306-45934-4.

[17] See Flashes in the Sky: Earth's Gamma-Ray Bursts Triggered by Lightning

[18] Yaffa Eliezer, Shalom Eliezer, The Fourth State of Matter: An Introduction to the Physics of Plasma, Publisher: Adam Hilger, 1989,
ISBN 978-0-85274-164-1, 226 pages, page 5

[19] Bittencourt, J.A. (2004). Fundamentals of Plasma Physics. Springer. p. 1. ISBN 9780387209753.

[20] Hong, Alice (2000). "Dielectric Strength of Air". The Physics Factbook.

[serway-22] ⁱ^j^k^l^mⁿ^o Raymond A. Serway (1998). Principles of Physics (2nd ed.). Fort Worth, Texas; London: Saunders College Pub. p. 602. ISBN 978-0-03-020457-9.

[Griffiths-23] David Griffiths (1999) [1981]. "7. Electrodynamics". In Alison Reeves. Introduction to Electrodynamics (3rd ed.). Upper Saddle River, New Jersey: Prentice Hall. p. 286. ISBN 978-0-13-805326-0. OCLC 40251748.

[24] Matula, R.A. (1979). "Electrical resistivity of copper, gold, palladium, and silver". Journal of Physical and Chemical Reference Data. 8 (4): 1147. Bibcode:1979JPCRD...8.1147M. doi:10.1063/1.555614.

[Giancoli-25] Douglas Giancoli (2009) [1984]. "25. Electric Currents and Resistance". In Jocelyn Phillips. Physics for Scientists and Engineers with Modern Physics (4th ed.). Upper Saddle River, New Jersey: Prentice Hall. p. 658. ISBN 978-0-13-149508-1.

[27] Copper wire tables : United States. National Bureau of Standards : Free Download & Streaming : Internet Archive. Archive.org (2001-03-10). Retrieved on 2014-02-03.

[30] Physical constants. (PDF format; see page 2, table in the right lower corner). Retrieved on 2011-12-17.

[31] 
Material properties of niobium.

[32] AISI 1010 Steel, cold drawn. Matweb

[33] "JFE steel" (PDF). Retrieved 2012-10-20.

[giancoli-34] Douglas C. Giancoli (1995). Physics: Principles with Applications (4th ed.). London: Prentice Hall. ISBN 978-0-13-102153-2.

(see also Table of Resistivity. hyperphysics.phy-astr.gsu.edu)

[35] John O'Malley (1992) Schaum's outline of theory and problems of basic circuit analysis, p. 19, McGraw-Hill Professional,
ISBN 0-07-047824-4

[37] Glenn Elert (ed.), "Resistivity of steel", The Physics Factbook, retrieved and archived 16 June 2011.

[39] Y. Pauleau, Péter B. Barna, P. B. Barna (1997) Protective coatings and thin films: synthesis, characterization, and applications, p. 215, Springer,
ISBN 0-7923-4380-8.

[Ohring-42] Milton Ohring (1995). Engineering materials science, Volume 1 (3rd ed.). Academic Press. p. 561. ISBN 978-0125249959.

[45] Physical properties of sea water. Kayelaby.npl.co.uk. Retrieved on 2011-12-17.

[47] [1]. chemistry.stackexchange.com

[Transmission_Lines_data-49] Transmission Lines data. Transmission-line.net. Retrieved on 2014-02-03.

[51] R. M. Pashley; M. Rzechowicz; L. R. Pashley; M. J. Francis (2005). "De-Gassed Water is a Better Cleaning Agent". The Journal of Physical Chemistry B. 109 (3): 1231–8. doi:10.1021/jp045975a. PMID 16851085.

[52] Lawrence S. Pan, Don R. Kania, Diamond: electronic properties and applications, p. 140, Springer, 1994
ISBN 0-7923-9524-7.

[53] S. D. Pawar; P. Murugavel; D. M. Lal (2009). "Effect of relative humidity and sea level pressure on electrical conductivity of air over Indian Ocean". Journal of Geophysical Research. 114: D02205. Bibcode:2009JGRD..11402205P. doi:10.1029/2007JD009716.

[54] E. Seran; M. Godefroy; E. Pili (2016). "What we can learn from measurements of air electric conductivity in 222Rn ‐ rich atmosphere". Earth and Space Science. 4 (2): 91–106. Bibcode:2017E&SS....4...91S. doi:10.1002/2016EA000241.

[55] Copper Wire Tables. US Dep. of Commerce. National Bureau of Standards Handbook. February 21, 1966

[56] M.R. Ward (1971) Electrical Engineering Science, pp. 36–40, McGraw-Hill.

[57] A. Matthiessen, Rep. Brit. Ass. 32, 144 (1862)

[58] A. Matthiessen, Progg. Anallen, 122, 47 (1864)

[59] J. Seymour (1972) Physical Electronics, chapter 2, Pitman

[60] Stephenson, C.; Hubler, A. (2015). "Stability and conductivity of self-assembled wires in a transverse electric field". Sci. Rep. 5: 15044. Bibcode:2015NatSR...515044S. doi:10.1038/srep15044. PMC 4604515. PMID 26463476.

[61] Otto H. Schmitt, University of Minnesota Mutual Impedivity Spectrometry and the Feasibility of its Incorporation into Tissue-Diagnostic Anatomical Reconstruction and Multivariate Time-Coherent Physiological Measurements. otto-schmitt.org. Retrieved on 2011-12-17.

搜尋此網誌

mjhjmtu

Electrical resistivity and conductivity

Contents

Definition

Ideal case

General scalar case

Tensor resistivity

Causes of conductivity

Band theory simplified

In metals

In semiconductors and insulators

In ionic liquids/electrolytes

Superconductivity

Plasma

Resistivity and conductivity of various materials

Temperature dependence

Linear approximation

Metals

Semiconductors

Complex resistivity and conductivity

Resistance versus resistivity in complicated geometries

Resistivity density products

See also

Notes

References

Further reading

External links

Popular posts from this blog

How to check contact read email or not when send email to Individual?

Displaying single band from multi-band raster using QGIS

How many registers does an x86_64 CPU actually have?