mjhjmtu

In mathematics, the radius of convergence of a power series is the radius of the largest disk in which the series converges. It is either a non-negative real number or ∞displaystyle infty . When it is positive, the power series converges absolutely and uniformly on compact sets inside the open disk of radius equal to the radius of convergence, and it is the Taylor series of the analytic function to which it converges.

Definition

For a power series ƒ defined as:

f(z)=∑n=0∞cn(z−a)n,displaystyle f(z)=sum _n=0^infty c_n(z-a)^n,

where

a is a complex constant, the center of the disk of convergence,

c_n is the n^th complex coefficient, and

z is a complex variable.

The radius of convergence r is a nonnegative real number or ∞displaystyle infty such that the series converges if

|z−a|<r<r,

and diverges if

|z−a|>r.displaystyle

Some may prefer an alternative definition, as existence is obvious:

r=supz−adisplaystyle r=sup leftz-a

On the boundary, that is, where |z − a| = r, the behavior of the power series may be complicated, and the series may converge for some values of z and diverge for others. The radius of convergence is infinite if the series converges for all complex numbers z.^[1]

Finding the radius of convergence

Two cases arise. The first case is theoretical: when you know all the coefficients cndisplaystyle c_n then you take certain limits and find the precise radius of convergence. The second case is practical: when you construct a power series solution of a difficult problem you typically will only know a finite number of terms in a power series, anywhere from a couple of terms to a hundred terms. In this second case, extrapolating a plot estimates the radius of convergence.

Theoretical radius

The radius of convergence can be found by applying the root test to the terms of the series. The root test uses the number

C=lim supn→∞|cn(z−a)n|n=lim supn→∞|cn|n|z−a|

"lim sup" denotes the limit superior. The root test states that the series converges if C < 1 and diverges if C > 1. It follows that the power series converges if the distance from z to the center a is less than

r=1lim supn→∞|cn|ndisplaystyle r=frac 1limsup _nrightarrow infty sqrt[n]c_n

and diverges if the distance exceeds that number; this statement is the Cauchy–Hadamard theorem. Note that r = 1/0 is interpreted as an infinite radius, meaning that ƒ is an entire function.

The limit involved in the ratio test is usually easier to compute, and when that limit exists, it shows that the radius of convergence is finite.

r=limn→∞|cncn+1|.displaystyle r=lim _nrightarrow infty left

This is shown as follows. The ratio test says the series converges if

limn→∞|cn+1(z−a)n+1||cn(z−a)n|<1.displaystyle lim _nto infty frac c_n+1(z-a)^n+1<1.

That is equivalent to

|z−a|<1limn→∞|cn+1||cn|=limn→∞|cncn+1|.displaystyle

Practical estimation of radius in the case of real coefficients

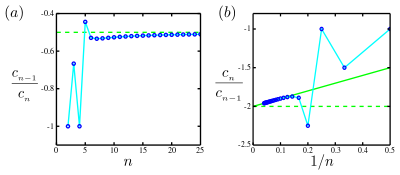
Domb–Sykes plot of the function f(ε)=ε(1+ε3)1+2ε.displaystyle f(varepsilon )=frac varepsilon (1+varepsilon ^3)sqrt 1+2varepsilon .^[2] On the left (a) is a straightforward plot of the ratio of the power-series coefficients cn−1/cndisplaystyle c_n-1/c_n as a function of index ndisplaystyle n; on the right, (b) is the Domb–Sykes plot of cn/cn−1displaystyle c_n/c_n-1 as a function of 1/ndisplaystyle 1/n. The solid green line is the straight-line asymptote in the Domb–Sykes plot, which intercepts the vertical axis at −2 and has a slope +1. Thus there is a singularity at ε=−1/2displaystyle varepsilon =-1/2 and so the radius of convergence is r=1/2.displaystyle r=1/2.

Usually, in scientific applications, only a finite number of coefficients cndisplaystyle c_n are known. Typically,^[vague] as ndisplaystyle n increases, these coefficients settle into a regular behavior determined by the nearest radius-limiting singularity. In this case, two main techniques have been developed, based on the fact that the coefficients of a Taylor series are roughly exponential with ratio 1/rdisplaystyle 1/r where r is the radius of convergence.

• The basic case is when the coefficients ultimately share a common sign or alternate in sign. As pointed out earlier in the article, in many cases the limit limn→∞cn/cn−1displaystyle lim _nto infty c_n/c_n-1 exists, and in this case 1/r=limn→∞cn/cn−1.displaystyle 1/r=lim _nto infty c_n/c_n-1. Negative rdisplaystyle r means the convergence-limiting singularity is on the negative axis. Estimate this limit, by plotting the cn/cn−1displaystyle c_n/c_n-1 versus 1/ndisplaystyle 1/n, and graphically extrapolate to 1/n=0displaystyle 1/n=0 (effectively n=∞displaystyle n=infty ) via a linear fit. The intercept with 1/n=0displaystyle 1/n=0 estimates the reciprocal of the radius of convergence, 1/rdisplaystyle 1/r. This plot is called a Domb–Sykes plot.


• The more complicated case is when the signs of the coefficients have a more complex pattern. Mercer and Roberts proposed the following procedure.^[3] Define the associated sequence

bn2=cn+1cn−1−cn2cncn−2−cn−12n=3,4,5,….displaystyle b_n^2=frac c_n+1c_n-1-c_n^2c_nc_n-2-c_n-1^2quad n=3,4,5,ldots .

Plot the finitely many known bndisplaystyle b_n versus 1/ndisplaystyle 1/n, and graphically extrapolate to 1/n=0displaystyle 1/n=0 via a linear fit.

The intercept with 1/n=0displaystyle 1/n=0 estimates the reciprocal of the radius of convergence, 1/rdisplaystyle 1/r.

This procedure also estimates two other characteristics of the convergence limiting singularity. Suppose the nearest singularity is of degree pdisplaystyle p and has angle ±θdisplaystyle pm theta to the real axis. Then the slope of the linear fit given above is −(p+1)/rdisplaystyle -(p+1)/r. Further, plot 12(cn−1bncn+cn+1cnbn)displaystyle frac 12left(frac c_n-1b_nc_n+frac c_n+1c_nb_nright) versus 1/n2displaystyle 1/n^2, then a linear fit extrapolated to 1/n2=0displaystyle 1/n^2=0 has intercept at cos⁡θdisplaystyle cos theta .

Radius of convergence in complex analysis

A power series with a positive radius of convergence can be made into a holomorphic function by taking its argument to be a complex variable. The radius of convergence can be characterized by the following theorem:

The radius of convergence of a power series ƒ centered on a point a is equal to the distance from a to the nearest point where ƒ cannot be defined in a way that makes it holomorphic.

The set of all points whose distance to a is strictly less than the radius of convergence is called the disk of convergence.

A graph of the functions explained in the text: Approximations in blue, circle of convergence in white

The nearest point means the nearest point in the complex plane, not necessarily on the real line, even if the center and all coefficients are real. For example, the function

f(z)=11+z2displaystyle f(z)=frac 11+z^2

has no singularities on the real line, since 1+z2displaystyle 1+z^2 has no real roots. Its Taylor series about 0 is given by

∑n=0∞(−1)nz2n.displaystyle sum _n=0^infty (-1)^nz^2n.

The root test shows that its radius of convergence is 1. In accordance with this, the function ƒ(z) has singularities at ±i, which are at a distance 1 from 0.

For a proof of this theorem, see analyticity of holomorphic functions.

A simple example

The arctangent function of trigonometry can be expanded in a power series familiar to calculus students:

arctan⁡(z)=z−z33+z55−z77+⋯.displaystyle arctan(z)=z-frac z^33+frac z^55-frac z^77+cdots .

It is easy to apply the root test in this case to find that the radius of convergence is 1.

A more complicated example

Consider this power series:

zez−1=∑n=0∞Bnn!zndisplaystyle frac ze^z-1=sum _n=0^infty frac B_nn!z^n

where the rational numbers B_n are the Bernoulli numbers. It may be cumbersome to try to apply the ratio test to find the radius of convergence of this series. But the theorem of complex analysis stated above quickly solves the problem. At z = 0, there is in effect no singularity since the singularity is removable. The only non-removable singularities are therefore located at the other points where the denominator is zero. We solve

ez−1=0displaystyle e^z-1=0,

by recalling that if z = x + iy and e ^iy = cos(y) + i sin(y) then

ez=exeiy=ex(cos⁡(y)+isin⁡(y)),displaystyle e^z=e^xe^iy=e^x(cos(y)+isin(y)),,

and then take x and y to be real. Since y is real, the absolute value of cos(y) + i sin(y) is necessarily 1. Therefore, the absolute value of e ^z can be 1 only if e ^x is 1; since x is real, that happens only if x = 0. Therefore z is pure imaginary and cos(y) + i sin(y) = 1. Since y is real, that happens only if cos(y) = 1 and sin(y) = 0, so that y is an integer multiple of 2π. Consequently the singular points of this function occur at

z = a nonzero integer multiple of 2πi.

The singularities nearest 0, which is the center of the power series expansion, are at ±2πi. The distance from the center to either of those points is 2π, so the radius of convergence is 2π.

Convergence on the boundary

If the power series is expanded around the point a and the radius of convergence is r, then the set of all points z such that |z − a| = r is a circle called the boundary of the disk of convergence. A power series may diverge at every point on the boundary, or diverge on some points and converge at other points, or converge at all the points on the boundary. Furthermore, even if the series converges everywhere on the boundary (even uniformly), it does not necessarily converge absolutely.

Example 1: The power series for the function ƒ(z) = 1/(1 − z), expanded around z = 0, which is simply

∑n=0∞zn,displaystyle sum _n=0^infty z^n,

has radius of convergence 1 and diverges at every point on the boundary.

Example 2: The power series for g(z) = −ln(1 − z), expanded around z = 0, which is

∑n=1∞1nzn,displaystyle sum _n=1^infty frac 1nz^n,

has radius of convergence 1, and diverges for z = 1 but converges for all other points on the boundary. The function ƒ(z) of Example 1 is the derivative of g(z).

Example 3: The power series

∑n=1∞1n2zndisplaystyle sum _n=1^infty frac 1n^2z^n

has radius of convergence 1 and converges everywhere on the boundary absolutely. If h is the function represented by this series on the unit disk, then the derivative of h(z) is equal to g(z)/z with g of Example 2. It turns out that h(z) is the dilogarithm function.

Example 4: The power series

∑i=1∞aizi where ai=(−1)n−12nn for n=⌊log2⁡(i)⌋+1, the unique integer with 2n−1≤i<2n,displaystyle sum _i=1^infty a_iz^itext where a_i=frac (-1)^n-12^nntext for n=lfloor log _2(i)rfloor +1text, the unique integer with 2^n-1leq i<2^n,

has radius of convergence 1 and converges uniformly on the entire boundary , but does not converge absolutely on the boundary.^[4]

Rate of convergence

If we expand the function

f(x)=sin⁡x=∑n=0∞(−1)n(2n+1)!x2n+1=x−x33!+x55!−⋯ for all xdisplaystyle f(x)=sin x=sum _n=0^infty frac (-1)^n(2n+1)!x^2n+1=x-frac x^33!+frac x^55!-cdots text for all x

around the point x = 0, we find out that the radius of convergence of this series is ∞displaystyle scriptstyle infty meaning that this series converges for all complex numbers. However, in applications, one is often interested in the precision of a numerical answer. Both the number of terms and the value at which the series is to be evaluated affect the accuracy of the answer. For example, if we want to calculate f(0.1) = sin(0.1) accurate up to five decimal places, we only need the first two terms of the series. However, if we want the same precision for x = 1 we must evaluate and sum the first five terms of the series. For f(10), one requires the first 18 terms of the series, and for f(100) we need to evaluate the first 141 terms.

So the fastest convergence of a power series expansion is at the center, and as one moves away from the center of convergence, the rate of convergence slows down until you reach the boundary (if it exists) and cross over, in which case the series will diverge.

Abscissa of convergence of a Dirichlet series

An analogous concept is the abscissa of convergence of a Dirichlet series

∑n=1∞anns.displaystyle sum _n=1^infty a_n over n^s.

Such a series converges if the real part of s is greater than a particular number depending on the coefficients a_n: the abscissa of convergence.

Notes

References

• 
  Brown, James; Churchill, Ruel (1989), Complex variables and applications, New York: McGraw-Hill, ISBN 978-0-07-010905-6
  


• 
  Stein, Elias; Shakarchi, Rami (2003), Complex Analysis, Princeton, New Jersey: Princeton University Press, ISBN 0-691-11385-8
  

External links

• What is radius of convergence?