mjhjmtu

A Helmholtz coil

Helmholtz coil schematic drawing

A Helmholtz coil is a device for producing a region of nearly uniform magnetic field, named after the German physicist Hermann von Helmholtz. It consists of two electromagnets on the same axis. Besides creating magnetic fields, Helmholtz coils are also used in scientific apparatus to cancel external magnetic fields, such as the Earth's magnetic field.

A beam of cathode rays in a vacuum tube bent into a circle by a Helmholtz coil

Description

A Helmholtz pair consists of two identical circular magnetic coils that are placed symmetrically along a common axis, one on each side of the experimental area, and separated by a distance hdisplaystyle h equal to the radius Rdisplaystyle R of the coil. Each coil carries an equal electric current in the same direction.^[1]

Setting h=Rdisplaystyle h=R, which is what defines a Helmholtz pair, minimizes the nonuniformity of the field at the center of the coils, in the sense of setting ∂2B/∂x2=0displaystyle partial ^2B/partial x^2=0^[2] (meaning that the first nonzero derivative is ∂4B/∂x4displaystyle partial ^4B/partial x^4 as explained below), but leaves about 7% variation in field strength between the center and the planes of the coils.
A slightly larger value of hdisplaystyle h reduces the difference in field between the center and the planes of the coils, at the expense of worsening the field's uniformity in the region near the center, as measured by ∂2B/∂x2displaystyle partial ^2B/partial x^2.^[3]

In some applications, a Helmholtz coil is used to cancel out the Earth's magnetic field, producing a region with a magnetic field intensity much closer to zero.^[4]

Mathematics

Magnetic field lines in a plane bisecting the current loops. Note the field is approximately uniform in between the coil pair. (In this picture the coils are placed one beside the other: the axis is horizontal.)

Magnetic field induction along the axis crossing the center of coils; z = 0 is the point in the middle of the distance between coils

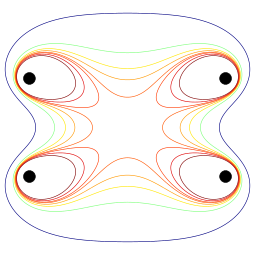
Contours showing the magnitude of the magnetic field near a coil pair, with one coil at top and the other at bottom. Inside the central "octopus", the field is within 1% of its central value B₀. The eight contours are for field magnitudes of 0.5 B₀, 0.8 B₀, 0.9 B₀, 0.95 B₀, 0.99 B₀, 1.01 B₀, 1.05 B₀, and 1.1 B₀.

The calculation of the exact magnetic field at any point in space is mathematically complex and involves the study of Bessel functions. Things are simpler along the axis of the coil-pair, and it is convenient to think about the Taylor series expansion of the field strength as a function of xdisplaystyle x, the distance from the central point of the coil-pair along the axis.
By symmetry, the odd-order terms in the expansion are zero. By arranging the coils so that the origin x=0displaystyle x=0 is an inflection point for the field strength due to each coil separately, one can guarantee that the order x2displaystyle x^2 term is also zero, and hence the leading non-constant term is of order x4displaystyle x^4. The inflection point for a simple coil is located along the coil axis at a distance R/2displaystyle R/2 from its centre. Thus the locations for the two coils are x=±R/2displaystyle x=pm R/2.

The calculation detailed below gives the exact value of the magnetic field at the center point. If the radius is R, the number of turns in each coil is n and the current through the coils is I, then the magnetic field B at the midpoint between the coils will be given by

B=(45)3/2μ0nIR,displaystyle B=left(frac 45right)^3/2frac mu _0nIR,

where μ0displaystyle mu _0 is the permeability of free space (4π×10−7 T⋅m/Adisplaystyle 4pi times 10^-7text Tcdot textm/A).

Derivation

Start with the formula for the on-axis field due to a single wire loop which is itself derived from the Biot–Savart law:^[5]

B1(x)=μ0IR22(R2+x2)3/2.displaystyle B_1(x)=frac mu _0IR^22(R^2+x^2)^3/2.

Here

μ0displaystyle mu _0; = the permeability constant = 4π×10−7 T⋅m/A=1.257×10−6 T⋅m/A,displaystyle 4pi times 10^-7text Tcdot textm/A=1.257times 10^-6text Tcdot textm/A,

Idisplaystyle I; = coil current, in amperes,

Rdisplaystyle R; = coil radius, in meters,

xdisplaystyle x; = coil distance, on axis, to point, in meters.

The Helmholtz coils consists of n turns of wire, so the equivalent current in a one-turn coil is n times the current I in the n-turn coil. Substituting nI for I in the above formula gives the field for an n-turn coil:

B1(x)=μ0nIR22(R2+x2)3/2.displaystyle B_1(x)=frac mu _0nIR^22(R^2+x^2)^3/2.

In a Helmholtz coil, a point halfway between the two loops has an x value equal to R/2, so calculate the field strength at that point:

B1(R2)=μ0nIR22(R2+(R/2)2)3/2.displaystyle B_1left(frac R2right)=frac mu _0nIR^22(R^2+(R/2)^2)^3/2.

There are also two coils instead of one (the coil above is at x=0; there is a second coil at x=R). From symmetry, the field strength at the midpoint will be twice the single coil value:

B(R2)=2B1(R/2)=2μ0nIR22(R2+(R/2)2)3/2=μ0nIR2(R2+(R/2)2)3/2=μ0nIR2(R2+14R2)3/2=μ0nIR2(54R2)3/2=(45)3/2μ0nIR=(855)μ0nIR.displaystyle beginalignedBleft(frac R2right)&=2B_1(R/2)\&=frac 2mu _0nIR^22(R^2+(R/2)^2)^3/2=frac mu _0nIR^2(R^2+(R/2)^2)^3/2\&=frac mu _0nIR^2(R^2+frac 14R^2)^3/2=frac mu _0nIR^2(frac 54R^2)^3/2\&=left(frac 45right)^3/2frac mu _0nIR\&=left(frac 85sqrt 5right)frac mu _0nIR.\endaligned

Time-varying magnetic field

Most Helmholtz coils use DC (direct) current to produce a static magnetic field. Many applications and experiments require a time-varying magnetic field. These applications include magnetic field susceptibility tests, scientific experiments, and biomedical studies (the interaction between magnetic field and living tissue). The required magnetic fields are usually either pulse or continuous sinewave. The magnetic field frequency range can be anywhere from near DC (0 Hz) to many kilohertz or even megahertz (MHz). An AC Helmholtz coil driver is needed to generate the required time-varying magnetic field. The waveform amplifier driver must be able to output high AC current to produce the magnetic field.

Driver voltage and current

Use the above equation in the mathematics section to calculate the coil current for a desired magnetic field, B.

I=(54)3/2(BRμ0n)displaystyle I=left(frac 54right)^3/2left(frac BRmu _0nright)

where μ0displaystyle mu _0 is the permeability of free space or 4π×10−7 T⋅m/A=1.257×10−6 T⋅m/A,displaystyle 4pi times 10^-7text Tcdot textm/A=1.257times 10^-6text Tcdot textm/A,

Idisplaystyle I; = coil current, in amperes,

Rdisplaystyle R; = coil radius, in meters,

n = number of turns in each coil.

Using a function generator and a high-current waveform amplifier driver to generate high-frequency Helmholtz magnetic field

Then calculate the required Helmholtz coil driver amplifier voltage:^[6]

V=I[ω(L1+L2)]2+(R1+R2)2displaystyle V=Isqrt bigl [omega bigl (L_1+L_2bigr )bigr ]^2+bigl (R_1+R_2bigr )^2

where

• 
  I is the peak current,


• 
  ω is the angular frequency or ω = 2πf,


• 
  L₁ and L₂ are the inductances of the two Helmholtz coils, and


• 
  R₁ and R₂ are the resistances of the two coils.

High-frequency series resonant

Generating a static magnetic field is relatively easy; the strength of the field is proportional to the current. Generating a high-frequency magnetic field is more challenging. The coils are inductors, and their impedance increases proportionally with frequency. To provide the same field intensity at twice the frequency requires twice the voltage across the coil. Instead of directly driving the coil with a high voltage, a series resonant circuit may be used to provide the high voltage.^[7] A series capacitor is added in series with the coils. The capacitance is chosen to resonate the coil at the desired frequency. Only the coils parasitic resistance remains. This method only works at frequencies close to the resonant frequency; to generate the field at other frequencies requires different capacitors. The Helmholtz coil resonant frequency, f0displaystyle f_0, and capacitor value, C, are given below.^[6]

f0=12π(L1+L2)Cdisplaystyle f_0=frac 12pi sqrt left(L_1+L_2right)C

C=1(2πf)2(L1+L2)displaystyle C=frac 1left(2pi fright)^2left(L_1+L_2right)

Maxwell coils

Helmholtz coils (hoops) on three perpendicular axes used to cancel the Earth's magnetic field inside the vacuum tank in a 1957 electron beam experiment

To improve the uniformity of the field in the space inside the coils, additional coils can be added around the outside. James Clerk Maxwell showed in 1873 that a third larger-diameter coil located midway between the two Helmholtz coils with the coil distance increased from coil radius Rdisplaystyle R to 3Rdisplaystyle sqrt 3R can reduce the variance of the field on the axis to zero up to the sixth derivative of position. This is sometimes called a Maxwell coil.

See also

• Maxwell coil


• Solenoid


• Halbach array


• A magnetic bottle has the same structure as Helmholtz coils, but with the magnets separated further apart so that the field expands in the middle, trapping charged particles with the diverging field lines. If one coil is reversed, it produces a cusp trap, which also traps charged particles.^[8]


• Helmholtz coils were designed and built for the Army Research Laboratory’s electromagnetic composite testing laboratory in 1993, for testing of composite materials to low-frequency magnetic fields.^[9]

References

External links

Wikimedia Commons has media related to Helmholtz coils.

• On-Axis Field of an Ideal Helmholtz Coil


• Axial field of a real Helmholtz coil pair


• 
  Helmholtz-Coil Fields by Franz Kraft, The Wolfram Demonstrations Project.


• Kevin Kuns (2007) Calculation of Magnetic Field inside Plasma Chamber, uses elliptic integrals and their derivatives to compute off-axis fields, from PBworks.


• 
  DeTroye, David J.; Chase, Ronald J. (November 1994), The Calculation and Measurement of Helmholtz Coil Fields (PDF), Army Research Laboratory, ARL-TN-35
  


• Magnetic Fields of Coils


• http://physicsx.pr.erau.edu/HelmholtzCoils/